BRSD ( KUBUS)

 MATA PELAJARAN : MATEMATIKA

KELAS : 8 ( DELAPAN) A

GURU PENGAMPU : SARI BUDI UTAMI, S.Pd

WAKTU PEMBELAJARAN : 31 Januari dan 3 Februari 2023

KOMPETENSI DASAR

3.9 Membedakan dan menentukan luas permukaan dan volume bangun ruang sisi datar (kubus, balok,  prisma,   dan limas)

 4.9 Menyelesaikan masalah yang berkaitan dengan luas permukaan dan volume bangun ruang sisi datar  (kubus,   balok,  prima dan    limas), serta gabungannya

Tujuan Pembelajaran :

Siswa dapat

Menentukan jaring-jaring kubus

Menentukan rumus luas sisi kubus

Menentukan luas permukaan kubus

Menghitung panjang diagonal sisi, diagonal ruang

Menghitung volume kubus

MATERI PEMBELAJARAN

Apa itu bangun ruang sisi datar?

Pernahkah kamu melihat benda-benda seperti berikut ini

disekitarmu?

Perhatikan gambar dadu, rubik, kado di atas? Berbentuk apakah benda-benda itu?

Pastinya     berbentuk    kubus.     Lalu    mengapa    benda-benda    tersebut berbentuk kubus dan apa yang dimaksud dengan kubus?

 1.      Pengertian Kubus

Perhatikan Gambar 2 secara seksama.

 Gambar tersebut menunjukkan sebuah bangu ruang yang semua sisinya berbentuk persegi dan semua rusuknya sama panjang. Bangun ruang seperti itu dinamakan kubus. Gambar 2 menunjukkan sebuah kubus ABCD.EFGH jadi dapat dikatakan bahwa kubus adalah bangun yang memiliki 6 sisi berbentuk persegi yang kongruen.

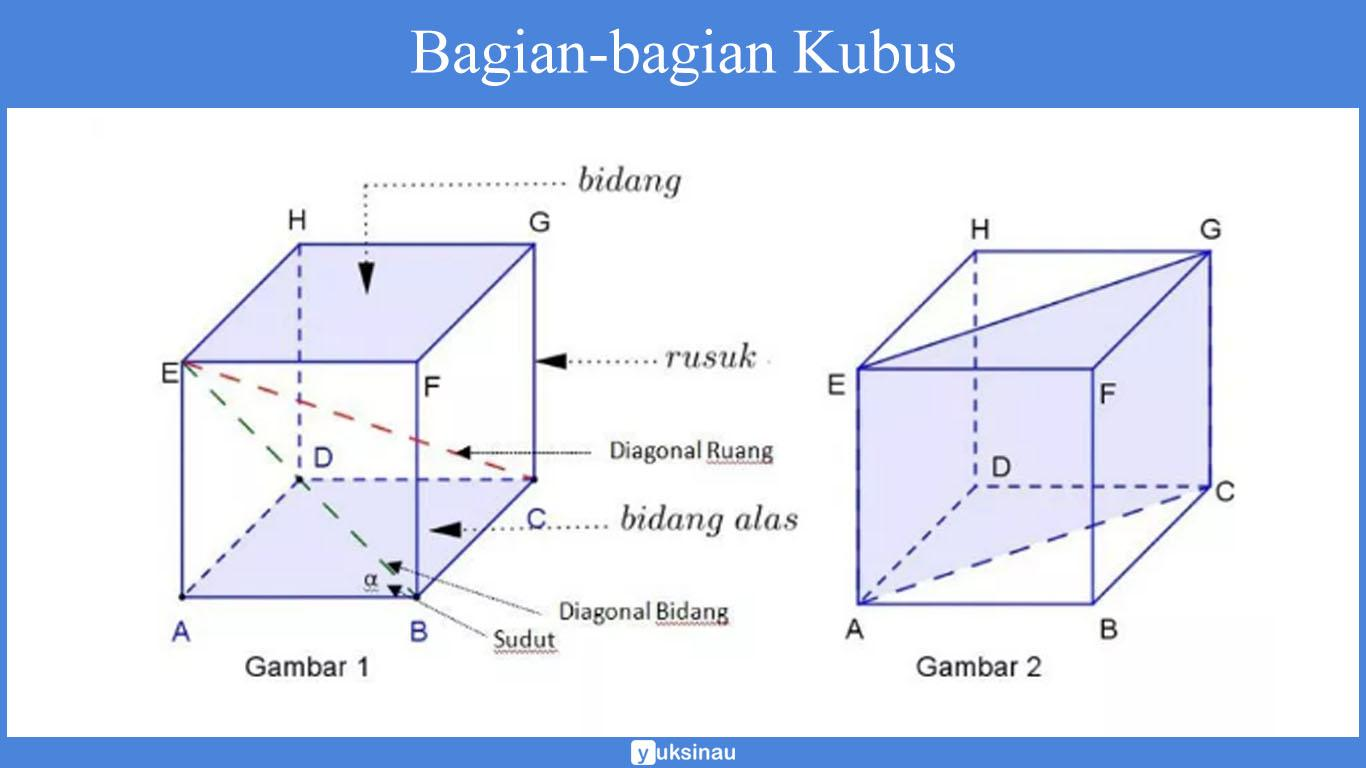
2.    Unsur-unsur Kubus

a.    Bidang atau Sisi

Bidang adalah daerah yang membatasi bagian luar dengan bagian dalam dari suatu bangun ruang. Perhatikan gambar 3 di bawah ini.

Kubus pada gambar diseri nama kubus ABCD.EFGH  bidang pada kubus ABCD.EFGH adalah bidang ABCD sebagai alas, bidang EFGH atas/tutup, bidang ADHE sebagai bidang kiri, bidang BCGF sebagai bidang kanan, bidang  ABFE sebagai bidang depan, dan DCGH sebagai bidang belakang. Jadi dapat disimpulkan bahwa kubus mempunyai 6 bidang yang semuanya berbentuk persegi.

b.    Rusuk

Rusuk kubus adalah garis potong antara dua sisi bidang kubus dan terlihat seperti kerangka yang menyusun kubus. Rusuk kubus ABCD.EFGH yaitu  AB, BC, CD, DA, EF, FG,  GH, HE, AE, BF, CG

dan DH.

c.   Titik sudut

Titik sudut kubus adalah titik potong antara dua rusuk. Kubus ABCD.EFGH memiliki 8 titik sudut, yaitu titik A, B, C, D, E, F, G, DAN H.

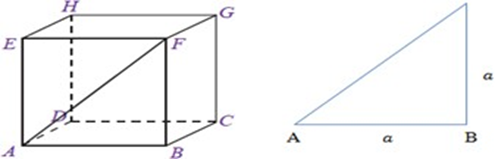
d.    Diagonal bidang

Jika titik E dan titik G dihubungkan, maka akan diperoleh garis EG. Begitupun jika titik A dan titik H dihubungkan akan diperoleh garis AH. Garis seperti EG dan AH inilah yang dinamakan diagonal bidang.

Dalam kubus, akan ditemukan 24 buah diagonaal bidang.

Pada gambar diatas, garis AF merupakan diagonal bidang dari kubus

ABCD.EFGH. Garis AF terletak pada bidang ABFE dan membagi bidang tersebut

menjadi dua buah segitiga siku-siku yaitu segitiga ABE dengan siku-siku di B, dan

segitiga AEF dengan siku-siku di E. Perhatikan segitiga ABE pada gambar dengan

AF sebagai diagonal bidang. Berdasarkan teorema Phytagoras, maka AF² = AB² + BF².

Misalkan panjang sisi kubus/rusuk adalah a, maka:

AF² = AB²+BF²

AF² = a²+a²

AF² = 2a²

AF = √2a²

AF = a√2

Semua bidang kubus berentuk persegi, maka panjang diagonal bidang dari setiap

bidang pada kubus nilainya sama. Sehingga jika a panjang rusuk sebuah kubus,

panjang diagonal bidang kubus 𝑎√2.

Contoh soal

Jika diketahui terdapat bangun ruang kubus yang mempunyai panjang rusuk sekitar 10 cm maka coba hitunglah diagonal sisi kubus dan diagonal ruang kubusnya.

Jawaban :

Jika diketahui  S = 10

Ditanyakan :

1.) Diagonal sisi kubus

2.) Diagonal ruang kubus

Penyelesaian :

1.) Diagonal sisi kubus

Ds = s√2

Maka :

Ds = 10√2

2.) Diagonal Ruang Kubus

Dr = s√3

Maka :

Dr = 10√3

e. Diagonal Ruang

Perhatikan gambar 6! Jika titik E dan titik C dihubungkan kita akan memperoleh

gsris EC, garis EC inilah yang dinamakan dengan diagonal ruang. Pada bidang

ABCD, terdapat diagonal bidang BD dengan panjang diagonal bidang adalah

𝑎√2. Dengan teorema phytagoras, dapat ditentukan pula panjang diagonal ruang

misalkan yang akan dicari adalah diagonal ruang BH. Panjang rusuk adalah a dan

bidang diagonal adalah 𝑎√2.

Panjang diagonal ruang BH adalah:

BH2 = DB2  + DH2

BH2  =𝑎√2² + 𝑎²

BH2 = 2𝑎² + 𝑎² 

BH2 = 3𝑎²

BH  = 𝑎√3.

Karena semua bidang dalam kubus berbentuk persegi, maka panjang diagonal

ruang setiap bidang kubus nilainya sama. Sehingga apabila a merupakan panjang

rusuk kubus, dengan 𝑎√2 panjang diagonal bidang maka panjang diagonal ruang

kubus 𝑎√3.

f. Bidang diagonal

Perhatikan kubus ABCD.EFGH dibaeah ini! Pada gambar tersebut, terlihat dua

buah diagonal bidang pada kubus ABCD.EFGH yaitu AC dan EG. Diagonal

bidang AC dan EG beserta dua rusuk kubus yang sejajae, yaitu AE dan CG

membentuk suatu bidang di dalam ruang kubus bidang ACGE pada kubus ABCD.

Bidang ACGE disebut sebagai bidang diagonal. Bidang diagonal adalah daerah

yang dibatasi oleh dua buah diagonal bidang dan dua buah rusuk yang saling

berhadapan dan sejajar yang membagi bangun ruang kubus menjadi dua bagian.

Gambar 7

Bidang diagonal ACGE berbentuk persegi, dengan panjang AC = 𝑎√2 (sebagai

diagonal bidang) dan AE = t.

Sehingga diperoleh:

LACGE = AC x AE

= 𝑎√2 x t

= t. 𝑎√2

3. Sifat-sifat Kubus

a. Kubus memiliki 6 sisi (bidang) berbentuk persegi yang saling kongruen. Sisi

(bidang) tersebut adalah bidang ABCD, ABFE, ECGF, CDHG, ADHE, dan

AFGH.

b. Kubus memiliki 12 buah rusuk yang sama panjang, yaitu AB, BF, FE, AE, BC,

AD, DC, HG, CG, DH, FG dan EH. Rusuk-rusuk AB, BC, CD, dan AD disebut

rusuk alas, sedangkan rusuk AE, BF, CG, dan DH disebut rusuk tegak. Rusukrusuk yang sejajar diantaranya AB//DC//EF//HG, AD//BC//EH//FG dan

AE//BF//CG//DH.

Rusuk-rusuk yang saling berpotongan diantaranya AB dengan AE, BC dengan

CG, dan EH dengan HD. Rusuk-rusuk yang saling bersilangan diantaranya AB

dengan CG, AD dengan BF, dan BC dengan DH.

c. Memiliki 8 titik sudut, yaitu A,B,C,D,E,F,G,H

d. Memiliki 12 diagonal bidang yang sama panjang, diantaranya adalah AC, BD,

AF, BE, BG, CF, AH, DE, DG, CH, EG, dan FH

e. Memiliki 4 diagonal ruang yang sama panjang dan berpotongan di satu titik, yaitu

AG, BH, CE dan DF

f. Memiliki 6 bidang diagonal persegi panjang yang saling kongruen, diantaranya

bidang ACGE, BGHA, AFGD, BEHC, ABGH, dan DCGH.

 Gambar Jaring-Jaring Kubus Beserta Unsur dan Rumus Luas Permukaan

 Jaring-jaring kubus adalah bangun datar dari bukaan bangun ruang menurut rusuknya. Jaring-jaring kubus terdiri dari enam buah persegi yang apabila digabungkan kembali akan membentuk kubus.

Amati jaring jaring kubus di bawah ini

Dengan demikian yang dimaksud jaring-jaring kubus adalah suatu rangkaian yang terdiri dari enam daerah persegi yang apabila digabungkan kembali (diimpitkan sisi-sisi perseginya) akan membentuk kubus. Jaring-jaring kubus terdiri dari enam buah persegi yang sama dan kongruen, maka untuk mencari luasnya menggunakan rumus luas jaring-jaring kubus yaitu 6s²

Rumus Luas Permukaan Kubus

Luas permukaan kubus adalah jumlah luas seluruh sisi pada suatu kubus atau sama dengan luas jaring-jaring kubus. Jumlah sisi kubus ada enam, maka rumus luas permukaan kubus adalah L = 6s² s adalah panjang sisi kubus.

Rumus Volume Kubus 

Volume kubus adalah ukuran ruang kubus yang dibatasi oleh sisi-sisi kubus. Untuk menghitung volume kubus, perlu diketahui panjang rusuk kubus. Jika rusuk kubus adalah r, maka rumus volume kubus adalah V = r³ 

 Contoh soal: 

1. Luas seluruh sisi kubus adalah 216 cm2, hitung volumenya. Pembahasan: Diketahui L = 216 cm2

Untuk menghitung volume kubus, perlu dicari panjang rusuknya terlebih dahulu menggunakan rumus luas permukaan kubus. 

L = 6s² 

216 = 6s²

 s² = 36 

s = √36 = 6

 Maka panjang rusuknya adalah 6 cm. Setelah itu, gunakan rumus volume kubus.

 V = r³ 

V = 6³ 

V = 216 cm³ 

Jadi, volume kubus adalah 216 cm3.

2 .Hitung luas permukaan kubus dengan panjang rusuk 10 cm.

 Pembahasan: 

Diketahui r = 10 cm 

L = 6r² 

L = 6×10²

 L = 6×100

 L = 600 cm²

 Jadi, luas permukaan kubus tersebut adalah 600 cm².

LATIHAN SOAL

1. Kubus adalah bangun ruang yang sisi-sisinya berbentuk ....

2. Perhatikan gambar di bawah ini !

Yang bukan merupakan jaring-jaring kubus adalah gambar ....

a. (I)

b. (II)

c. (III)

d. (IV)

3. 

Empat macam rangkaian enam bujur sangkar di atas, yang merupakan jaring-jaring kubus adalah...

A. (1)

B. (2)

C. (3)

D. (4)

4.  Pak win menyusun kardus-kardus berisi gelas di lantai tokonya. Susunan kardus gelas itu berbentuk balok berukuran panjang 6 kardus, lebar 4 kardus, dan tinggi 4 kardus. Menurutmu, berapa jumlah kardus gelas yang disusun pak win ?

5. Dito, anak pak win, menyusun kubus-kubus mainannya menjadi kubus yang lebih besar. Panjang sisi kubus besar itu 5 kubus mainan. Berapa jumlah kubus mainan yang digunakan ditto untuk membuat kubus besar itu ?