MATA PELAJARAN : MATEMATIKA
KELAS : 7 ( TUJUH) A-B-C-D
GURU PENGAMPU : SARI BUDI UTAMI, S.Pd
WAKTU PEMBELAJARAN : 16 - 20 Januari 2023
KOMPETENSI DASAR
3.10 Menganalisis hubungan antar sudut sebagai akibat dari dua garis sejajar yang dipotong oleh garis transversal
4.10 Menyelesaikan masalah yang berkaitan dengan hubungan antar sudut sebagai akibat dari dua garis sejajar yang dipotong oleh garis transversal
Tujuan Pembelajaran :
Setelah mengukuti kegiatan pembelajaran menggunakan model pembelajaran discovery Learning, dengan metode literasi, eksperimen, praktikum, dan presentasi dengan menumbuhkan sikap menyadari kebesaran Tuhan, sikap gotong royong, jujur, dan berani mengemukakan pendapat, siswa dapat :
- Membagi garis menjadi beberapa bagian sama panjang
- Menghitung panjang garis
MATERI PEMBELAJARAN
Perbandingan Segmen Garis
Sebuah garis dapat dibagi menjadi n bagian yang sama panjang atau dengan perbandingan tertentu. Perhatikan Gambar di bawah ini.
Gambar tersebut menunjukkan garis PQ dibagi menjadi 5 bagian yang sama panjang, sehingga PK = KL = LM = MN = NQ. Jika dari titik K, L, M, N, dan Q ditarik garis vertikal ke bawah, sedemikian sehingga PA = AB = BC = CD = DE maka diperoleh sebagai berikut.
PM : MQ = 3 : 2
PC : CE = 3 : 2
maka
PM : MQ = PC : CE
QN : NP = 1 : 4
ED : DP = 1 : 4
maka,
QN : NP = ED : DP
PL : PQ = 2 : 5
PB : PE = 2 : 5
maka
PL : PQ = PB : PE
QL : QP = 3 : 5
EB : EP = 3 : 5
maka:
QL : QP = EB : EP
Berdasarkan uraian tersebut, secara umum dapat disimpulkan sebagai berikut. Pada Δ ABC di bawah ini berlaku perbandingan sebagai berikut.
AD : DB = AE : EC atau AD/ DB = AE / EC
AD : AB = AE : AC atau AD / AB = AE / AC
BD : DA = CE : EA atau BD / DA = CE / EA
BD : BA = CE : CA atau BD / BA = CE / CA
AD : AB = AE : AC = DE : BC atau AD / AB = AE / AC = DE / BC
Contoh soal tentang perbandingan garis
Contoh 1:
Pada gambar di atas, diketahui QR // TS. Jika PR = 15 cm, PQ = 12 cm,
dan PS = 10 cm, tentukan
panjang PT;
perbandingan panjang TS dan QR.
Penyelesaian:
PS/PR = PT/PQ
10 cm/15 cm = PT / 12 cm
PT = 10x 12/15 cm
PT = 120 cm/15
PT = 8 cm
Jadi, panjang PT = 8 cm.
PT / PQ = TS/QR
8/12 = TS/QR
2/3 = TS/QR
Jadi, TS : QR = 2 : 3.
Contoh 2:
Penyelesaian:
Perhatikan bahwa AB : AC = 2 : 3 atau dapat dinyatakan sebagai AB/AC = 2/3 . AB/AC=2/3.
Dengan demikian, diperoleh:
Jadi, panjang AC adalah 6 cm.
Contoh 3:
Pada ruas garis AB, terletak titik P di antara A dan B, sehingga AP : PB = 1 : 5. Jika panjang AB = 12 cm, maka panjang AP adalah...
Penyelesaian:
Diketahui titik P berada di antara A dan B, sehingga AB = AP + PB. Oleh karena AP : PB = 1 : 5, maka AB = AP + PB = 6 . Dengan demikian, AP : AB = 1 : 6 atau dapat dinyatakan sebagai AP/AB = 1/6. AP/AB =1/6. Dengan demikian, diperoleh:
Jadi, panjang AP adalah 2 cm.
LATIHAN
1. Pada gambar di atas, diketahui RS // TU. Jika UV = 9 cm, VT = 6 cm, VS = 3 cm dan UV : VS =
VT : VR. Tentukan panjang VR.
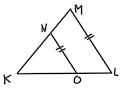
2. Pada gambar diatas garis NO//ML dan panjang KN = 12 cm, OL = 12 cm dan KL = 26 cm.
Maka panjang KM adalah……..
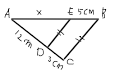
3. Diketahui gambar sebagai berikut.
Jika garis DE//CB, maka nilai x pada gambar diatas adalah…







Tidak ada komentar:
Posting Komentar