BRSD ( KUBUS)

 MATA PELAJARAN : MATEMATIKA

KELAS : 8 ( DELAPAN) A

GURU PENGAMPU : SARI BUDI UTAMI, S.Pd

WAKTU PEMBELAJARAN : 31 Januari dan 3 Februari 2023

KOMPETENSI DASAR

3.9 Membedakan dan menentukan luas permukaan dan volume bangun ruang sisi datar (kubus, balok,  prisma,   dan limas)

 4.9 Menyelesaikan masalah yang berkaitan dengan luas permukaan dan volume bangun ruang sisi datar  (kubus,   balok,  prima dan    limas), serta gabungannya

Tujuan Pembelajaran :

Siswa dapat

Menentukan jaring-jaring kubus

Menentukan rumus luas sisi kubus

Menentukan luas permukaan kubus

Menghitung panjang diagonal sisi, diagonal ruang

Menghitung volume kubus

MATERI PEMBELAJARAN

Apa itu bangun ruang sisi datar?

Pernahkah kamu melihat benda-benda seperti berikut ini

disekitarmu?

Perhatikan gambar dadu, rubik, kado di atas? Berbentuk apakah benda-benda itu?

Pastinya     berbentuk    kubus.     Lalu    mengapa    benda-benda    tersebut berbentuk kubus dan apa yang dimaksud dengan kubus?

 1.      Pengertian Kubus

Perhatikan Gambar 2 secara seksama.

 Gambar tersebut menunjukkan sebuah bangu ruang yang semua sisinya berbentuk persegi dan semua rusuknya sama panjang. Bangun ruang seperti itu dinamakan kubus. Gambar 2 menunjukkan sebuah kubus ABCD.EFGH jadi dapat dikatakan bahwa kubus adalah bangun yang memiliki 6 sisi berbentuk persegi yang kongruen.

2.    Unsur-unsur Kubus

a.    Bidang atau Sisi

Bidang adalah daerah yang membatasi bagian luar dengan bagian dalam dari suatu bangun ruang. Perhatikan gambar 3 di bawah ini.

Kubus pada gambar diseri nama kubus ABCD.EFGH  bidang pada kubus ABCD.EFGH adalah bidang ABCD sebagai alas, bidang EFGH atas/tutup, bidang ADHE sebagai bidang kiri, bidang BCGF sebagai bidang kanan, bidang  ABFE sebagai bidang depan, dan DCGH sebagai bidang belakang. Jadi dapat disimpulkan bahwa kubus mempunyai 6 bidang yang semuanya berbentuk persegi.

b.    Rusuk

Rusuk kubus adalah garis potong antara dua sisi bidang kubus dan terlihat seperti kerangka yang menyusun kubus. Rusuk kubus ABCD.EFGH yaitu  AB, BC, CD, DA, EF, FG,  GH, HE, AE, BF, CG

dan DH.

c.   Titik sudut

Titik sudut kubus adalah titik potong antara dua rusuk. Kubus ABCD.EFGH memiliki 8 titik sudut, yaitu titik A, B, C, D, E, F, G, DAN H.

d.    Diagonal bidang

Jika titik E dan titik G dihubungkan, maka akan diperoleh garis EG. Begitupun jika titik A dan titik H dihubungkan akan diperoleh garis AH. Garis seperti EG dan AH inilah yang dinamakan diagonal bidang.

Dalam kubus, akan ditemukan 24 buah diagonaal bidang.

Pada gambar diatas, garis AF merupakan diagonal bidang dari kubus

ABCD.EFGH. Garis AF terletak pada bidang ABFE dan membagi bidang tersebut

menjadi dua buah segitiga siku-siku yaitu segitiga ABE dengan siku-siku di B, dan

segitiga AEF dengan siku-siku di E. Perhatikan segitiga ABE pada gambar dengan

AF sebagai diagonal bidang. Berdasarkan teorema Phytagoras, maka AF² = AB² + BF².

Misalkan panjang sisi kubus/rusuk adalah a, maka:

AF² = AB²+BF²

AF² = a²+a²

AF² = 2a²

AF = √2a²

AF = a√2

Semua bidang kubus berentuk persegi, maka panjang diagonal bidang dari setiap

bidang pada kubus nilainya sama. Sehingga jika a panjang rusuk sebuah kubus,

panjang diagonal bidang kubus 𝑎√2.

Contoh soal

Jika diketahui terdapat bangun ruang kubus yang mempunyai panjang rusuk sekitar 10 cm maka coba hitunglah diagonal sisi kubus dan diagonal ruang kubusnya.

Jawaban :

Jika diketahui  S = 10

Ditanyakan :

1.) Diagonal sisi kubus

2.) Diagonal ruang kubus

Penyelesaian :

1.) Diagonal sisi kubus

Ds = s√2

Maka :

Ds = 10√2

2.) Diagonal Ruang Kubus

Dr = s√3

Maka :

Dr = 10√3

e. Diagonal Ruang

Perhatikan gambar 6! Jika titik E dan titik C dihubungkan kita akan memperoleh

gsris EC, garis EC inilah yang dinamakan dengan diagonal ruang. Pada bidang

ABCD, terdapat diagonal bidang BD dengan panjang diagonal bidang adalah

𝑎√2. Dengan teorema phytagoras, dapat ditentukan pula panjang diagonal ruang

misalkan yang akan dicari adalah diagonal ruang BH. Panjang rusuk adalah a dan

bidang diagonal adalah 𝑎√2.

Panjang diagonal ruang BH adalah:

BH2 = DB2  + DH2

BH2  =𝑎√2² + 𝑎²

BH2 = 2𝑎² + 𝑎² 

BH2 = 3𝑎²

BH  = 𝑎√3.

Karena semua bidang dalam kubus berbentuk persegi, maka panjang diagonal

ruang setiap bidang kubus nilainya sama. Sehingga apabila a merupakan panjang

rusuk kubus, dengan 𝑎√2 panjang diagonal bidang maka panjang diagonal ruang

kubus 𝑎√3.

f. Bidang diagonal

Perhatikan kubus ABCD.EFGH dibaeah ini! Pada gambar tersebut, terlihat dua

buah diagonal bidang pada kubus ABCD.EFGH yaitu AC dan EG. Diagonal

bidang AC dan EG beserta dua rusuk kubus yang sejajae, yaitu AE dan CG

membentuk suatu bidang di dalam ruang kubus bidang ACGE pada kubus ABCD.

Bidang ACGE disebut sebagai bidang diagonal. Bidang diagonal adalah daerah

yang dibatasi oleh dua buah diagonal bidang dan dua buah rusuk yang saling

berhadapan dan sejajar yang membagi bangun ruang kubus menjadi dua bagian.

Gambar 7

Bidang diagonal ACGE berbentuk persegi, dengan panjang AC = 𝑎√2 (sebagai

diagonal bidang) dan AE = t.

Sehingga diperoleh:

LACGE = AC x AE

= 𝑎√2 x t

= t. 𝑎√2

3. Sifat-sifat Kubus

a. Kubus memiliki 6 sisi (bidang) berbentuk persegi yang saling kongruen. Sisi

(bidang) tersebut adalah bidang ABCD, ABFE, ECGF, CDHG, ADHE, dan

AFGH.

b. Kubus memiliki 12 buah rusuk yang sama panjang, yaitu AB, BF, FE, AE, BC,

AD, DC, HG, CG, DH, FG dan EH. Rusuk-rusuk AB, BC, CD, dan AD disebut

rusuk alas, sedangkan rusuk AE, BF, CG, dan DH disebut rusuk tegak. Rusukrusuk yang sejajar diantaranya AB//DC//EF//HG, AD//BC//EH//FG dan

AE//BF//CG//DH.

Rusuk-rusuk yang saling berpotongan diantaranya AB dengan AE, BC dengan

CG, dan EH dengan HD. Rusuk-rusuk yang saling bersilangan diantaranya AB

dengan CG, AD dengan BF, dan BC dengan DH.

c. Memiliki 8 titik sudut, yaitu A,B,C,D,E,F,G,H

d. Memiliki 12 diagonal bidang yang sama panjang, diantaranya adalah AC, BD,

AF, BE, BG, CF, AH, DE, DG, CH, EG, dan FH

e. Memiliki 4 diagonal ruang yang sama panjang dan berpotongan di satu titik, yaitu

AG, BH, CE dan DF

f. Memiliki 6 bidang diagonal persegi panjang yang saling kongruen, diantaranya

bidang ACGE, BGHA, AFGD, BEHC, ABGH, dan DCGH.

 Gambar Jaring-Jaring Kubus Beserta Unsur dan Rumus Luas Permukaan

 Jaring-jaring kubus adalah bangun datar dari bukaan bangun ruang menurut rusuknya. Jaring-jaring kubus terdiri dari enam buah persegi yang apabila digabungkan kembali akan membentuk kubus.

Amati jaring jaring kubus di bawah ini

Dengan demikian yang dimaksud jaring-jaring kubus adalah suatu rangkaian yang terdiri dari enam daerah persegi yang apabila digabungkan kembali (diimpitkan sisi-sisi perseginya) akan membentuk kubus. Jaring-jaring kubus terdiri dari enam buah persegi yang sama dan kongruen, maka untuk mencari luasnya menggunakan rumus luas jaring-jaring kubus yaitu 6s²

Rumus Luas Permukaan Kubus

Luas permukaan kubus adalah jumlah luas seluruh sisi pada suatu kubus atau sama dengan luas jaring-jaring kubus. Jumlah sisi kubus ada enam, maka rumus luas permukaan kubus adalah L = 6s² s adalah panjang sisi kubus.

Rumus Volume Kubus 

Volume kubus adalah ukuran ruang kubus yang dibatasi oleh sisi-sisi kubus. Untuk menghitung volume kubus, perlu diketahui panjang rusuk kubus. Jika rusuk kubus adalah r, maka rumus volume kubus adalah V = r³ 

 Contoh soal: 

1. Luas seluruh sisi kubus adalah 216 cm2, hitung volumenya. Pembahasan: Diketahui L = 216 cm2

Untuk menghitung volume kubus, perlu dicari panjang rusuknya terlebih dahulu menggunakan rumus luas permukaan kubus. 

L = 6s² 

216 = 6s²

 s² = 36 

s = √36 = 6

 Maka panjang rusuknya adalah 6 cm. Setelah itu, gunakan rumus volume kubus.

 V = r³ 

V = 6³ 

V = 216 cm³ 

Jadi, volume kubus adalah 216 cm3.

2 .Hitung luas permukaan kubus dengan panjang rusuk 10 cm.

 Pembahasan: 

Diketahui r = 10 cm 

L = 6r² 

L = 6×10²

 L = 6×100

 L = 600 cm²

 Jadi, luas permukaan kubus tersebut adalah 600 cm².

LATIHAN SOAL

1. Kubus adalah bangun ruang yang sisi-sisinya berbentuk ....

2. Perhatikan gambar di bawah ini !

Yang bukan merupakan jaring-jaring kubus adalah gambar ....

a. (I)

b. (II)

c. (III)

d. (IV)

3. 

Empat macam rangkaian enam bujur sangkar di atas, yang merupakan jaring-jaring kubus adalah...

A. (1)

B. (2)

C. (3)

D. (4)

4.  Pak win menyusun kardus-kardus berisi gelas di lantai tokonya. Susunan kardus gelas itu berbentuk balok berukuran panjang 6 kardus, lebar 4 kardus, dan tinggi 4 kardus. Menurutmu, berapa jumlah kardus gelas yang disusun pak win ?

5. Dito, anak pak win, menyusun kubus-kubus mainannya menjadi kubus yang lebih besar. Panjang sisi kubus besar itu 5 kubus mainan. Berapa jumlah kubus mainan yang digunakan ditto untuk membuat kubus besar itu ?

SUDUT

  MATA PELAJARAN : MATEMATIKA

KELAS : 7 ( TUJUH) A-B-C-D

GURU PENGAMPU : SARI BUDI UTAMI, S.Pd

WAKTU PEMBELAJARAN : 30 Januari - 3 Februari 2023

 

KOMPETENSI DASAR

3.10         Menganalisis hubungan antar sudut sebagai akibat dari dua garis sejajar yang dipotong oleh garis transversal

4.10         Menyelesaikan masalah yang berkaitan dengan hubungan antar sudut sebagai akibat dari dua garis sejajar yang dipotong oleh garis transversal

 

Tujuan Pembelajaran :

• Siswa dapat memahami pengertian sudut dan jenis-jenis sudut

• Siswa dapat mengukur besar sudut dengan busur derajat

• Siswa dapat menjelaskan perbedaan jenis sudut (siku, lancip, tumpul)

MATERI PEMBELAJARAN

Sudut

sudut dapat diartikan sebagai sebuah daerah yang terbentuk karena adanya dua buah garis sinar yang titik pangkalnya saling bersekutu atau berhimpit.

Sudut dalam geometri merupakan suatu besaran rotasi suatu ruas garis dari satu titik pangkalnya ke posisi yang lain.

Pengertian sudut ialah dua buah garis sinar yang membentuk suatu daerah karena titik pangkalnya saling berhimpit atau bersekutu. Sudut tersebut memiliki bagian bagiannya sendiri.

Berikut bagian bagian pada sudut yaitu meliputi:

Sudut mempunyai tiga bagian penting, diantaranya yaitu:

Kaki Sudut

Kaki sudut ialah garis sinar yang digunakan untuk menciptakan sudut.

Merupakan garis sinar yang membentuk sudut tersebut.

Titik Sudut

Titik sudut ialah titik potong atau titik pangkal yang digunakan garis sinar untuk saling berhimpitan.

Merupakan titik pangkal atau  titik potong tempat berhimpitnya garis sinar.

Daerah Sudut

Daerah atau ruang yang terdapat diantara dua kaki sudut.

Daerah sudut ialah ruang atau daerah yang terdapat di antara dua buah kaki sudutnya.

Jenis-jenis Sudut

Untuk menyatakan besaran pada suatu sudut maka memakai satuan derajat (°), menit (‘), dan juga detik (“), di mana:

• Sudut yang besarnya 90° disebut sebagai sudut siku-siku.
• Sudut yang besarnya 180° disebut sebagai sudut lurus.
• Sudut yang besarnya antara 0° serta 90° disebut sebagai sudut lancip.
• Sudut yang besarnya antara 90° serta 180° (90°< D < 180°) disebut sebagai sudut tumpul.
• Sudut yang besarnya lebih dari 180° serta kurang dari 360° (180° < D < 360°) disebut sebagai sudut refleks.
• Jumlah dua sudut yang saling berpelurus (bersuplemen) yaitu 180°. Sudut yang satu adalah pelurus dari sudut yang lain.
• Jumlah dua sudut yang saling berpenyiku (berkomplemen) yaitu 90°. Sudut yang satu adalah penyiku dari sudut yang lain.
• Apabila dua garis berpotongan maka dua sudut yang letaknya saling membelakangi titik potongnya disebut sebagai dua sudut yang saling bertolak belakang. Dua sudut yang saling bertolak belakang merupakan sudut yang sama besar.

Hubungan Antara Dua Sudut

 Jika dua buah sudut digabungkan menjadi satu maka akan membentuk hubungan seperti di bawah ini:

 

Sudut Berpenyiku

Dua buah sudut yang berhimpitan akan menghasilkan bentuk sudut siku siku sehingga salah satu sudut dijadikan sebagai sudut penyiku diantara kedua sudut tadi. Dengan begitu dua buah sudut yang berhimpitan tersebut dapat dikatakan sebagai sudut komplemen atau berpenyiku. Untuk lebih paham mengenai sudut berpenyiku ini maka dapat anda perhatikan gambar di bawah ini:

Sudut Berpelurus

Hubungan dua sudut selanjutnya ialah sudut berpelurus. Jika dua sudut saling berhimpitan maka akan menghasilkan sudut lurus, dimana salah satu sudut dijadikan sebagai sudut pelurus untuk sudut lainnya. Maka dari itu hubungan dua buah sudut tersebut dapat dinamakan dengan sudut suplemen atau sudut berpelurus. Untuk lebih jelasnya  perhatikan gambar di bawah ini:

CONTOH

1. Perhatikan gambar di bawah ini!

Hitunglah besar pelurus sudut ABD?

Jawab.

Sudut berpelurus memiliki besar sudut 180⁰.

Maka,

(2x + 10)⁰ + (x + 8)⁰ = 180⁰

     2x + x + 10⁰ + 8⁰ = 180⁰

                   3x + 18⁰ = 180⁰

                            3x = 180⁰ – 18⁰

                            3x = 162⁰

                              x = 54⁰

Besar sudut pelurus ABD = besar sudut CBD, sehingga:

∠CBD = x + 8⁰ = 54⁰ + 8⁰ = 62⁰

Jadi, besar sudut pelurus ABD ialah 62⁰.

2. Perhatikan gambar di bawah ini

Tentukan besar sudut a dan b, untuk:

a. b = 2a

b. a = b – 20°

c. b = 3a –30°

d. b = 3a + 20°

Penyelesaian:

a. b = 2a, maka:

∠a + ∠b = 90°

a + 2a = 90°

3a = 90°

a = 30°

b = 2a

b = 2.30°

b = 60°

b. a = b – 20°, maka

∠a + ∠b = 90°

b – 20° + b = 90°

2b = 110°

b = 55°

a = b – 20°

a = 55° - 20°

a = 35°

c. b = 3a –30°, maka:

∠a + ∠b = 90°

a + 3a –30° = 90°

4a = 120°

a = 30°

b = 3a –30°

b = 3.30° –30°

b = 90° –30°

b = 60°

d. b = 3a + 20°, maka:

∠a + ∠b = 90°

a + 3a + 20° = 90°

4a = 70°

a = 17,5°

b = 3a + 20°

b = 3.17,5° + 20°

b = 52,5° + 20°

b = 72,5°

LATIHAN SOAL

1. Besar sudut penyiku dari sudut 35⁰ adalah…….

A. 55⁰

B. 65⁰

C. 145⁰

D. 325⁰

2. Perhatikan gambar berikut

Besar penyiku ∠ PSR adalah

A. 9⁰

B. 32⁰

C. 48⁰

D. 58⁰

3. Perhatikan gambar di bawah ini

Besar ∠ABD adalah ….

A. 98°    

B. 105°      

C. 112°       

D. 119°

4. Perhatikan gambar di bawah ini

Besar pelurus sudut SQR adalah ….

A. 101°      

B. 100°      

C. 95°                  

D. 92°

5. Perhatikan gambar

Besar ∠BCA adalah ….

A. 70°    

B. 100°      

C. 110°       

D. 154°

POSTEST KELAS 8

 MATA PELAJARAN : MATEMATIKA

KELAS : 8 ( DELAPAN) A

GURU PENGAMPU : SARI BUDI UTAMI, S.Pd

WAKTU PEMBELAJARAN : 24 Januari 2023

KOMPETENSI DASAR

3.6 Menjelaskan dan membuktikan teorema Pythagoras dan tripel Pythagoras

4.6  Menyelesaikan masalah yang berkaitan dengan teorema Pythagoras dan tripel Pythagoras

Tujuan Pembelajaran :

• Siswa dapat megerjakan soal postest dengan baik dan benar

SOAL POSTEST TERDOKUMENTASI PADA PERANGKAT

SUDUT

 MATA PELAJARAN : MATEMATIKA

KELAS : 7 ( TUJUH) A-B-C-D

GURU PENGAMPU : SARI BUDI UTAMI, S.Pd

WAKTU PEMBELAJARAN : 23 - 27 Januari 2023

 

KOMPETENSI DASAR

3.10         Menganalisis hubungan antar sudut sebagai akibat dari dua garis sejajar yang dipotong oleh garis transversal

4.10         Menyelesaikan masalah yang berkaitan dengan hubungan antar sudut sebagai akibat dari dua garis sejajar yang dipotong oleh garis transversal

 

Tujuan Pembelajaran :

• Siswa dapat memahami pengertian sudut dan jenis-jenis sudut

• Siswa dapat mengukur besar sudut dengan busur derajat

• Siswa dapat menjelaskan perbedaan jenis sudut (siku, lancip, tumpul)

MATERI PEMBELAJARA

Sudut

Pengertian sudut ialah dua buah garis sinar yang membentuk suatu daerah karena titik pangkalnya saling berhimpit atau bersekutu. Sudut tersebut memiliki bagian bagiannya sendiri. Berikut bagian bagian pada sudut yaitu meliputi:

Kaki sudut ialah garis sinar yang digunakan untuk menciptakan sudut.

Titik sudut ialah titik potong atau titik pangkal yang digunakan garis sinar untuk saling berhimpitan.

Daerah sudut ialah ruang atau daerah yang terdapat di antara dua buah kaki sudutnya.

Hubungan Antara Dua Sudut

 Jika dua buah sudut digabungkan menjadi satu maka akan membentuk hubungan seperti di bawah ini:

 

Sudut Berpenyiku

Dua buah sudut yang berhimpitan akan menghasilkan bentuk sudut siku siku sehingga salah satu sudut dijadikan sebagai sudut penyiku diantara kedua sudut tadi. Dengan begitu dua buah sudut yang berhimpitan tersebut dapat dikatakan sebagai sudut komplemen atau berpenyiku. Untuk lebih paham mengenai sudut berpenyiku ini maka dapat anda perhatikan gambar di bawah ini:

Sudut Berpelurus

Hubungan dua sudut selanjutnya ialah sudut berpelurus. Jika dua sudut saling berhimpitan maka akan menghasilkan sudut lurus, dimana salah satu sudut dijadikan sebagai sudut pelurus untuk sudut lainnya. Maka dari itu hubungan dua buah sudut tersebut dapat dinamakan dengan sudut suplemen atau sudut berpelurus. Untuk lebih jelasnya  perhatikan gambar di bawah ini:

CONTOH

1. Perhatikan gambar di bawah ini!

Hitunglah besar pelurus sudut ABD?

Jawab.

Sudut berpelurus memiliki besar sudut 180⁰.

Maka,

(2x + 10)⁰ + (x + 8)⁰ = 180⁰

     2x + x + 10⁰ + 8⁰ = 180⁰

                   3x + 18⁰ = 180⁰

                            3x = 180⁰ – 18⁰

                            3x = 162⁰

                              x = 54⁰

Besar sudut pelurus ABD = besar sudut CBD, sehingga:

∠CBD = x + 8⁰ = 54⁰ + 8⁰ = 62⁰

Jadi, besar sudut pelurus ABD ialah 62⁰.

2. Perhatikan gambar di bawah ini

Tentukan besar sudut a dan b, untuk:

a. b = 2a

b. a = b – 20°

c. b = 3a –30°

d. b = 3a + 20°

Penyelesaian:

a. b = 2a, maka:

∠a + ∠b = 90°

a + 2a = 90°

3a = 90°

a = 30°

b = 2a

b = 2.30°

b = 60°

b. a = b – 20°, maka

∠a + ∠b = 90°

b – 20° + b = 90°

2b = 110°

b = 55°

a = b – 20°

a = 55° - 20°

a = 35°

c. b = 3a –30°, maka:

∠a + ∠b = 90°

a + 3a –30° = 90°

4a = 120°

a = 30°

b = 3a –30°

b = 3.30° –30°

b = 90° –30°

b = 60°

d. b = 3a + 20°, maka:

∠a + ∠b = 90°

a + 3a + 20° = 90°

4a = 70°

a = 17,5°

b = 3a + 20°

b = 3.17,5° + 20°

b = 52,5° + 20°

b = 72,5°

LATIHAN SOAL

1. Besar sudut penyiku dari sudut 35⁰ adalah…….

A. 55⁰

B. 65⁰

C. 145⁰

D. 325⁰

2. Perhatikan gambar berikut

Besar penyiku ∠ PSR adalah

A. 9⁰

B. 32⁰

C. 48⁰

D. 58⁰

3. Perhatikan gambar di bawah ini

Besar ∠ABD adalah ….

A. 98°    

B. 105°      

C. 112°       

D. 119°

4. Perhatikan gambar di bawah ini

Besar pelurus sudut SQR adalah ….

A. 101°      

B. 100°      

C. 95°                  

D. 92°

5. Perhatikan gambar

Besar ∠BCA adalah ….

A. 70°    

B. 100°      

C. 110°       

D. 154°

 

PENERAPAN TEOREMA PYTHAGORAS

MATA PELAJARAN : MATEMATIKA

KELAS : 8 ( DELAPAN) A

GURU PENGAMPU : SARI BUDI UTAMI, S.Pd

WAKTU PEMBELAJARAN : 17 dan 20 Januari 2023

KOMPETENSI DASAR

3.6 Menjelaskan dan membuktikan teorema Pythagoras dan tripel Pythagoras

4.6  Menyelesaikan masalah yang berkaitan dengan teorema Pythagoras dan tripel Pythagoras

Tujuan Pembelajaran :

• Siswa dapat menghitung panjang diagonal bangun datar

• Siswa dapat menyelesaikan Masalah dalam kehidupan nyata.

• Siswa dapat menyelesaikan masalah yang berkaitan dengan penerapan terorema Pythagoras tripel Pythagoras

MATERI PEMBELAJARAN

Penerapan Teorema Pythagoras Dalam Kehidupan Sehari-Hari

Banyak sekali permasalahan dalam kehidupan sehari-hari yang disajikan dalam bentuk soal cerita dan dapat diselesaikan dengan menggunakan teorema Pythagoras.

Untuk memudahkan menyelesaikan soal-soal penerapan teorema Pythagoras diperlukan bantuan gambar (sketsa). Untuk mengetahui manfaat teorema Pythagoras silahkan pelajari contoh soal di bawah ini.

Contoh Soal 1

Seorang anak menaikkan layang-layang dengan benang yang panjangnya 250 meter. Jarak anak di tanah dengan titik yang tepat berada di bawah layang-layang adalah 70 meter. Hitunglah ketinggian layang-layang tersebut.

Penyelesaian:

Jika digambarkan sketsanya, akan tampak seperti gambar di bawah ini.

Di mana AB merupakan jarak anak di tanah dengan titik yang tepat berada di bawah layang-layang dan AC merupakan panjang benang. Tinggi langyang-layang dapat dicari dengan teorema Pythagoras yakni:

BC = √(AC2 – AB2)

BC = √(2502 – 702)

BC = √(62500 – 4900)

BC = √57600

BC = 240 m

Jadi, ketinggian layang-layang tersebut adalah 240 m

Contoh Soal 2

Seorang anak akan mengambil sebuah layang-layang yang tersangkut di atas sebuah tembok yang berbatasan langsung dengan sebuah kali. Anak tersebut ingin menggunakan sebuah tangga untuk mengambil layang-layang tersebut dengan cara meletakan kaki tangga di pinggir kali. Jika lebar kali tersebut 5 meter dan tinggi tembok 12 meter, hitunglah panjang tangga minimal yang diperlukan agar ujung tangga bertemu dengan bagian atas tembok.

Penyelesaian:

Jika digambarkan sketsanya, akan tampak seperti gambar di bawah ini.

Di mana XY merupakan jarak kaki tangga dengan bawah tembok (lebar kali) dan YZ merupakan tinggi tembok, maka panjang tangga (XZ) dapat dicari dengan teorema Pythagoras yakni:

XZ = √(XY2 + YZ2)

XZ = √(52 + 122)

XZ = √(25 + 144)

XZ = √169

XZ = 13 m

Jadi, panjang tangga minimal yang diperlukan agar ujung tangga bertemu dengan bagian atas tembok adalah 13 m.

  

LATIHAN

1. Dua buah tiang berdampingan berjarak 24 m. Jika tinggi tiang masing-masing adalah 22 m dan 12 m, hitunglah panjang kawat penghubung antara ujung tiang tersebut.

2. Sebuah tiang bendera akan di isi kawat penyangga agar tidak roboh seperti gambar di bawah ini.

Jika jarak kaki tiang dengan kaki kawat penyangga adalah 8 m, jarak kaki tiang dengan ujung kawat penyangga pertama 6 m dan jarak kawat penyangga pertama dengan kawat penyangga kedua adalah 9 m. Hitunglah panjang total kawat yang diperlukan dan hitunglah biaya yang diperlukan jika harga kawat Rp 25.000 per meter!

3. Persegi panjang ABCD memiliki panjang diagonal 50 cm. Jika lebar persegi panjang tersebut adalah 30 cm, maka luasnya adalah……

4. Perhatikan gambar trapesium di bawah ini.

Panjang sisi miring RS dari trapesium tersebut adalah………

5. Sebuah segitiga siku-siku memiliki panjang sisi terpendeknya berturut-turut adalah 8 cm dan 15 cm. Panjang hipotenusa dari segitiga tersebut……….

PERBANDINGAN SEGMEN GARIS

MATA PELAJARAN : MATEMATIKA

KELAS : 7 ( TUJUH) A-B-C-D

GURU PENGAMPU : SARI BUDI UTAMI, S.Pd

WAKTU PEMBELAJARAN : 16 - 20 Januari 2023

KOMPETENSI DASAR

3.10         Menganalisis hubungan antar sudut sebagai akibat dari dua garis sejajar yang dipotong oleh garis transversal

4.10         Menyelesaikan masalah yang berkaitan dengan hubungan antar sudut sebagai akibat dari dua garis sejajar yang dipotong oleh garis transversal

 

Tujuan Pembelajaran :

Setelah mengukuti kegiatan pembelajaran menggunakan model pembelajaran discovery Learning, dengan metode literasi, eksperimen, praktikum, dan presentasi dengan menumbuhkan sikap menyadari kebesaran Tuhan, sikap gotong royong, jujur, dan berani mengemukakan pendapat, siswa dapat :

•    Membagi garis menjadi beberapa bagian sama panjang
•    Menghitung panjang garis 

MATERI PEMBELAJARAN 

Perbandingan Segmen Garis

Sebuah garis dapat dibagi menjadi n bagian yang sama panjang atau dengan perbandingan tertentu. Perhatikan Gambar di bawah ini.

Gambar tersebut menunjukkan garis PQ dibagi menjadi 5 bagian yang sama panjang, sehingga PK = KL = LM = MN = NQ. Jika dari titik K, L, M, N, dan Q ditarik garis vertikal ke bawah, sedemikian sehingga PA = AB = BC = CD = DE maka diperoleh sebagai berikut.

PM : MQ = 3 : 2

PC : CE = 3 : 2

maka

PM : MQ = PC : CE

QN : NP = 1 : 4

ED : DP = 1 : 4

maka,

QN : NP = ED : DP

PL : PQ = 2 : 5

PB : PE = 2 : 5

maka

PL : PQ = PB : PE

QL : QP = 3 : 5

EB : EP = 3 : 5

maka:

QL : QP = EB : EP

Berdasarkan uraian tersebut, secara umum dapat disimpulkan sebagai berikut. Pada Δ ABC di bawah ini berlaku perbandingan sebagai berikut.

AD : DB = AE : EC atau AD/ DB = AE / EC

AD : AB = AE : AC atau AD / AB = AE / AC

BD : DA = CE : EA atau BD / DA  = CE / EA

BD : BA = CE : CA atau BD / BA  = CE / CA

AD : AB = AE : AC = DE : BC atau AD / AB = AE / AC = DE / BC

Contoh soal tentang perbandingan garis

Contoh 1:

Pada gambar di atas, diketahui QR // TS. Jika PR = 15 cm, PQ = 12 cm,

dan PS = 10 cm, tentukan

panjang PT;

perbandingan panjang TS dan QR.

 

Penyelesaian:

PS/PR = PT/PQ

10 cm/15 cm = PT / 12 cm

PT = 10x 12/15 cm

PT = 120 cm/15

PT = 8 cm

Jadi, panjang PT = 8 cm.

PT / PQ = TS/QR

8/12 = TS/QR

2/3 = TS/QR

Jadi, TS : QR = 2 : 3.

Contoh 2:

Perbandingan ruas garis AB : AC = 2 : 3. Jika panjang AB = 4 cm, maka panjang AC adalah ....

Penyelesaian:

Perhatikan bahwa AB : AC = 2 : 3 atau dapat dinyatakan sebagai  AB/AC = 2/3 . AB/AC=2/3. 

Dengan demikian, diperoleh:

Jadi, panjang AC adalah 6 cm.

Contoh 3:

Pada ruas garis AB, terletak titik P di antara A dan B, sehingga AP : PB = 1 : 5. Jika panjang AB = 12 cm, maka panjang AP adalah...

Penyelesaian:

Diketahui titik P berada di antara A dan B, sehingga AB = AP + PB. Oleh karena AP : PB = 1 : 5, maka AB = AP + PB = 6 . Dengan demikian, AP : AB = 1 : 6 atau dapat dinyatakan sebagai AP/AB = 1/6. AP/AB =1/6. Dengan demikian, diperoleh:

Jadi, panjang AP adalah 2 cm.

LATIHAN

1.  Pada gambar di atas, diketahui RS // TU. Jika UV = 9 cm, VT = 6 cm, VS = 3 cm dan UV : VS =

      VT : VR. Tentukan panjang VR.

2. Pada gambar diatas garis NO//ML dan panjang KN = 12 cm, OL = 12 cm dan KL = 26 cm.

     Maka  panjang KM adalah……..

3. Diketahui gambar sebagai berikut.

Jika garis DE//CB, maka nilai x pada gambar diatas adalah…

HUBUNGAN ANTAR PANJANG SISI SEGITIGA SIKU SIKU

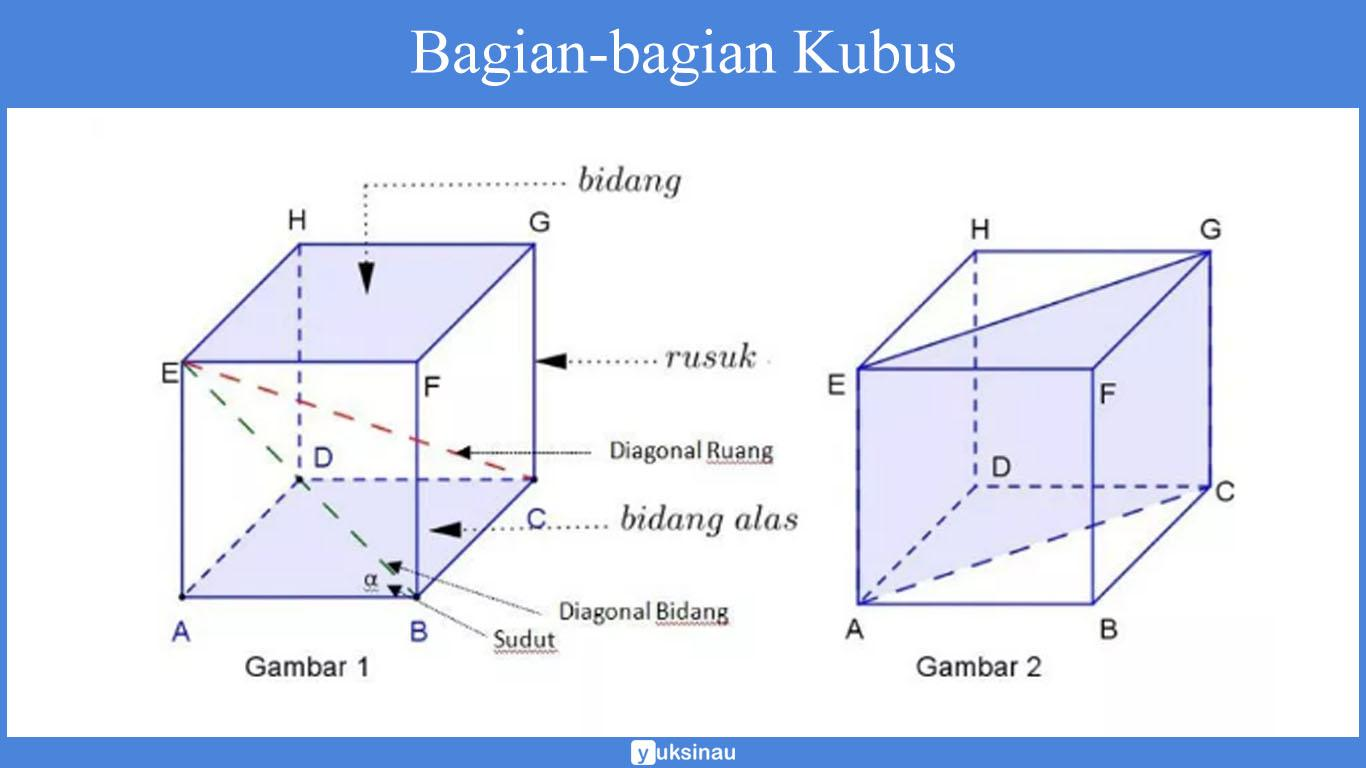
 Hari/ Tanggal : Selasa dan Jumat, 10-13 Januari 2023

 Kelas              : 8A 

 Materi            :  Teorema Pythagoras

KOMPETENSI DASAR

3.6 Menjelaskan dan membuktikan teorema Pythagoras dan tripel Pythagoras

4.6  Menyelesaikan masalah yang berkaitan dengan teorema Pythagoras dan tripel Pythagoras

Tujuan Pembelajaran :

Setelah mengukuti kegiatan pembelajaran menggunakan model pembelajaran discovery Learning, dengan metode literasi, eksperimen, praktikum, dan presentasi dengan menumbuhkan sikap menyadari kebesaran Tuhan, sikap gotong royong, jujur, dan berani mengemukakan pendapat, siswa dapat :

• Memjelaskan sisi-sisi pada segitiga siku-siku

• Memahami 3 bilangan yang merupakan panjang sisi-sisi segitiga siku-siku

• Menuliskan tiga bilangan ukuran panjang sisi segitga siku-siku (Triple Pythagoras).

Assalamualaikum anak- anak yang sholeh sholehah....

Apa kabarnya hari ini ?

Semoga kita semua dalam lindungan Allah SWT Aamiin.....

Dan jangan lupa tetap selalu menjaga kesehatan dan selalu memakai prokes nya ya nak.

Baiklah sebelum kita melaksanakan pembelajaran di pagi ini, alangkah baiknya kita awali dengan melaksanakan sholat dhuha dan murojaahnya terlebih dahulu ya nak, dan tak lupa setelah itu pembacaan asmaul husna dan doa belajar ya supaya ilmu yang dipelajari hari ini akan bermanfaat, mudah diterima dan akan berkah ilmunya 

Baiklah untuk pertemuan kali ini kita akan memasuki materi 

HUBUNGAN ANTAR PANJANG SISI SEGITIGA SIKU SIKU

Menentukan Macam-Macam Segitiga

Tanpa perlu mengetahui gambar/ilustrasi suatu segitiga, berdasarkan teorema Pythagoras dapat diketahui kategori suatu segitiga.

Pada pembahasan mengenai segiempat dan segitiga, telah dijelaskan kalau ada beberapa macam segitiga berdasarkan sudut dan kesamaan sisinya.

Namun secara garis besar, bisa dibilang hanya ada tiga jenis segitiga.

Segitiga tersebut merupakan segitiga lancip dengan sudut kurang dari 90°.

Segitiga siku-siku yang salah satu sudutnya membentuk 90°.

Dan segitiga tumpul yang salah satu sudutnya lebih besar dari 90°.

Pada segitiga lancip, persamaan pada teorema Pythagoras tidak terpenuhi.

Sebab ekspresinya berubah menjadi sebuah pertidaksamaan, yaitu berupa a2 + b2 > c2.

Artinya jumlah kuadrat dari dua sisi yang membentuk sudut lancip tersebut, lebih besar dari kuadrat panjang sisi lainnya (yaitu c).

Hal serupa tapi berbeda tanda berlaku pada segitiga tumpul. Jumlah kuadrat dari dua sisi yang membentuk sudut tumpul kurang dari kuadrat panjang sisi lainnya, yaitu i>a2 + b2 < c2.

Dan tanda kesamaan akan berlaku ketika segitiganya merupakan segitiga siku-siku.

Dari itu semua, bisa diringkas kondisi-kondisinya menjadi seperti berikut:

a2 + b2 = c2, segitiga siku-siku, sudutnya 90°.

a2 + b2 > c2, segitiga tumpul, sudutnya > 90°.

a2 + b2 < c2, segitiga lancip, sudutnya < 90°.

Perbandingan Panjang Sisi-Sisi pada Segitiga Siku-Siku Khusus

Terdapat dua segitiga siku-siku khusus yaitu segitiga siku-siku sama kaki dan segitiga siku-siku dengan salah satu sudutnya 30°. Bagaimana perbandingan sisi-sisi kedua segitiga tersebut? Dengan konsep Teorema Pythagoras, kita akan menemukan perbandingannya.

1. Segitiga Siku-siku Sama Kaki

Salah satu dari segitiga siku-siku adalah segitiga siku-siku sama kaki dengan besar ketiga sudutnya adalah 45° - 45° - 90°. Setiap segitiga siku-siku sama kaki adalah setengah dari persegi.

Perbandingan segitiga siku siku sama sisi (sudut 45°)

Pada segitiga siku-siku sama kaki maka kedua kaki sudutnya sama panjang. Oleh karena itu, dengan memisahkan panjang kaki sudutnya 1 satuan, maka panjang hipotenusanya dapat ditentukan dengan menggunakan teorema Pythagoras. 

2. Perbandingan Sisi Sudut 30° dan 60°

Perbandingan segitiga dengan sudut 30°,60° dan 90°

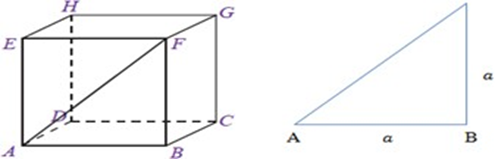
Segitiga ABC tersebut adalah segitiga sama sisi, jika dipotong menjadi dua bagian maka terdapat dua segitiga siku-siku, seperti gambar berikut. 

Jika panjang AC = 2 cm dan panjang CD = 1 cm maka, 

Jadi, perbandingan segitiga dengan sudut 30°,60° dan 90° adalah

CONTOH

1 – Soal Perbandingan Sisi Segitiga Siku-Siku

Panjang sisi AC adalah ….

A. 4√2 cm

B. 4√3 cm

C. 8 cm

D. 8√3 cm

Pemabahasan:

Pada soal terdapat sebuah segitiga siku-siku dengan beberapa informasi seperti berikut.

Panjang sisi AB = 4 cm

Besar sudut A: ∠A = 60o

Segitiga siku-siku di sudut B (besar sudut B: ∠B = 90o)

Besar sudut C: ∠C = 180o ‒ (90o + 60o) = 30o

Diketahui perbandingan besar sudut A : B : C = 60o : 90o : 30o, sehingga perbandingan sisi segitiga siku-siku adalah AB : BC : AC = 1 : √3 : 2.

Menghitung panjang sisi AC:

AC/AB = 2/1

AC/4 = 2/1

1 × AC = 4 × 2

AC = 8 cm

Jadi, panjang sisi AC sama dengan cm

Jawaban: C

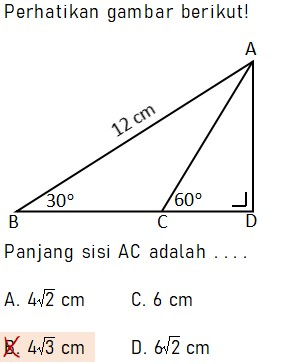
2 – Soal Perbandingan Sisi Segitiga Siku-Siku

Pembahasan:

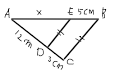
Dari soal dapat diketahui dua buah sergitiga siku-siku yaitu segitiga ABD dan ACD yang keduanya siku-siku di titik D (besar ∠ADB = ∠ADC = 90o). Di mana besar sudut dan panjang sisi yang diketahui sesuai dengan nilai-nilai di bawah

Besar sudut ABD: ∠ABD = 30o 

Besar sudut ACD: ∠ACD = 60o

Panjang sisi AB = 12 cm

Sehingga dapat diketahui bahwa besar ∠BAD = 60o dan besar ∠CAD = 60o. Maka perbandingan sisi segitiga untuk kedua segitiga tersebut adalah,

∠ABD : ∠BDA : ∠BAD = 30o : 90o : 60o 

AD : AB : BD = 1 : 2 : √3

∠ACD : ∠CDA : ∠CAD = 60o : 90o : 30o

AD : AC : CD = √3 : 2 : 1

Dapat diperoleh dua perbandingan sisi segitiga siku-siku yaitu,

AD : AB = 1 : 2

AD : AC = √3 : 2.

Menentukan hubungan panjang sisi AD dan AC:

AD : AC = √3 : 2

AD/AC = √3/2

AD = √3/2AC

Menghitung nilai AC:

AD : AB = 1 : 2

AD : 12 = 1 : 2

AD/12 = 1/2

2 × AD = 1 × 12

2 × √3/2AC = 1 × 12

√3AC = 12

AC = 12/√3 = 12/3√3 = 4√3 cm

Jadi, panjang sisi AC sama dengan 4√3 cm.

Jawaban: B

LATIHAN

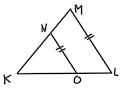
1. Diketahui segitiga PQR siku-siku di P dan besar sudut Q adalah . Jika panjang PQ = 7 cm, maka panjang PR dan QR adalah....

2. Perhatikan segitiga siku-siku di bawah ini.

Panjang sisi AC adalah ... cm