MATA PELAJARAN : MATEMATIKA
KELAS : 9C,9D
MATERI : KESEBANGUNAN DAN KEKONGRUENAN
PERTEMUAN : KE 1 DARI 4
GURU PENGAMPU : SARI BUDI UTAMI, S.Pd
WAKTU PEMBELAJARAN : 2 X 40 MENIT
HARI/TANGGAL . : SENIN, 15 JANUARI 2024
KD
3.6 Menjelaskan dan menentukan kesebangunan dan kekongruenan antar bangun datar
Tujuan Pembelajaran
Melalui pendekatan saintifik dengan menggunakan model pembelajaran discovery Learning, dengan metode literasi, dan presentasi peserta didik diharapkan
- Menjelaskan Kesebangunan dua bangun datar
Assalamualaikum anak- anak yang sholeh sholehah....
Apa kabarnya hari ini ?
Semoga kita semua dalam lindungan Allah SWT Aamiin.....
Dan jangan lupa tetap selalu menjaga kesehatan nya ya nak.
Baiklah sebelum kita melaksanakan pembelajaran di pagi ini, alangkah baiknya kita awali dengan melaksanakan sholat dhuha dan murojaahnya terlebih dahulu ya nak, dan tak lupa setelah itu pembacaan asmaul husna dan doa belajar ya supaya ilmu yang dipelajari hari ini akan bermanfaat, mudah diterima dan akan berkah ilmunya
Baiklah sebelum kita melanjutkan materi pada hari ini, mari kita ulas sedikit materi minggu kemarin yaitu tentang bangun datar, Nah untuk pertemuan kali ini kita akan memasuki materi
Dua Bangun Datar yang Sebangun

Sekarang, coba kamu perhatikan Gambar di atas! Sebangunkah persegipanjan ABCD dengan persegipanjang EFGH? Pada persegipanjang ABCD dan persegipanjang EFGH, perbandingan panjangnya adalah 4 : 8 = 1 : 2.
Adapun perbandingan lebarnya adalah 2 : 4 = 1 : 2. Dengan demikian, perbandingan sisi-sisi yang bersesuaian pada kedua persegipanjang tersebut dapat dinyatakan sebagai berikut.
Kemudian, perhatikan sudut-sudut yang bersesuaian pada persegipanjang ABCD dan persegipanjang EFGH. Oleh karena keduanya berbentuk persegipanjang, setiap sudut besarnya 90° sehingga sudut-sudut yang bersesuaian pada kedua bangun tersebut sama besar.
Artinya kedua persegi panjang tersebut memiliki sisi-sisi yang bersesuaian dan sebanding sedangkan sudut-sudut yang bersesuaian sama besar. Oleh karena itu, persegipanjang ABCD dan persegipanjang EFGH dikatakan sebangun.
Kesebangunan adalah kesamaan perbandingan panjang sisi dan besar sudut antara dua buah bangun datar atau lebih.
Dua bangun datar yang sebangun

Kemudian, perhatikan sudut-sudut yang bersesuaian pada persegipanjang ABCD dan persegipanjang KLMN. Oleh karena keduanya berbentuk persegipanjang, setiap sudut besarnya 90° sehingga sudut-sudut yang bersesuaian pada kedua bangun tersebut sama besar.
Syarat Kesebangunan
Jadi, dua atau lebih bangun dikatakan sebangun jika memenuhi syarat-syarat sebagai berikut.
- Panjang sisi-sisi yang bersesuaian pada bangun-bangun tersebut memiliki perbandingan yang senilai.
- Sudut-sudut yang bersesuaian pada bangun-bangun tersebut sama besar.
Pengertian Kekongruenan
Kekongruenan merupakan dua buah bangun datar yang di mana kedua bangunnya sama – sama memiliki bentuk dan juga ukuran yang sama.
Kekongruenan ini biasa dilambangkan dengan pemakaian simbol ≅.
Perhatikan contoh di bawah ini:
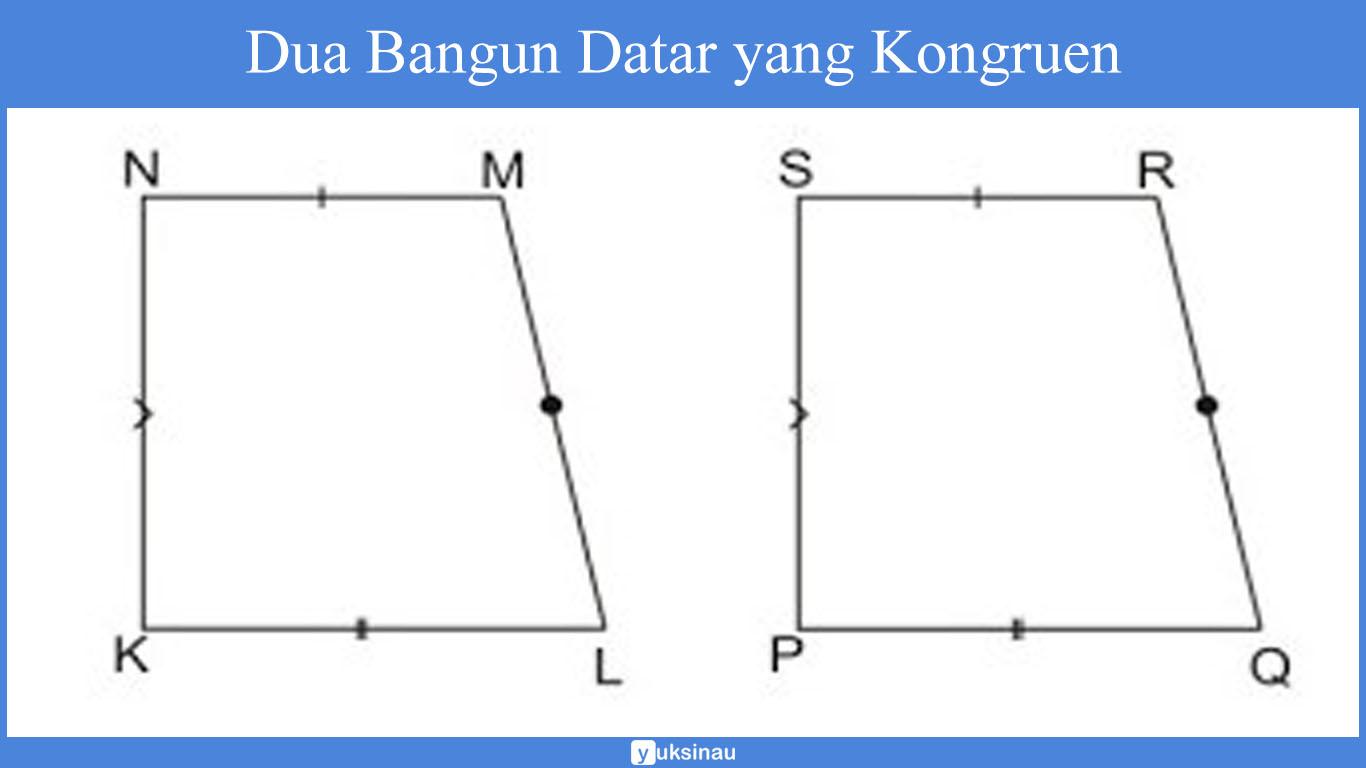
1. Dua Bangun Datar yang Kongruen
Pada kedua bangun di atas adalah bangun yang kongruen, karena panjang KL = PQ, Panjang LM = QR, panjang MN = RS, panjang NK = SP maka oleh karena itu, pada bangun KLMN dan PQRS dapat dikatakan adalah kongruen karena memiliki bentuk dan ukuran yang sama.
Perbedaan Kesebangunan dan Kekongruenan
Hal mendasar yang membedakan kongruen dan sebangun yaitu:
Bangun dikatakan kongruen jika sisi-sisi yang bersesuaian harus sama panjang. Sementaa jika bangun dikatakan sebangun apabila perbandingan sisi-sisi yang bersesuaian harus sama besar.
Sehingga dapat kita simpulkan bahwa, seluruh bangun yang kongruen sudah pasti sebangun, namun jika sebangun belum tentu kongruen.
CONTOH
1. Berikut ini ditampilkan ukuran panjang dan lebar dari 4 buah persegipanjang.
(i) 10 cm, 15 cm
(ii) 16 cm, 20 cm
(iii) 18 cm, 12 cm
(iv) 12 cm, 15 cm
Pasangan persegipanjang yang sebangun adalah….
A. (i) dan (ii)
B. (ii) dan (iii)
C. (i) dan (iv), (ii) dan (iii)
D. (i) dan (iii), (ii) dan (iv)
Pembahasan
Persegipanjang yang sebangun akan memiliki perbandingan panjang dan lebar yang sama:
(i) 10 cm, 15 cm → 2 : 3
(ii) 16 cm, 20 cm → 4 : 5
(iii) 18 cm, 12 cm → 3 : 2
(iv) 12 cm, 15 cm → 4 : 5
Terlihat yang sebangun adalah (i) dan (iii) serta (ii) dan (iv), jawaban D.
2. Perhatikan gambar dua buah belah ketupat di bawah ini, apakah kedua berdiri tersebut sanggup dinyatakan kongruen?
Penyelesaian:
Untuk menjawab soal tersebut, kalian harus mengingat kembali akan sifat-sifat berdiri datar yang dimiliki oleh belah ketupat, yaitu:
a. Semua sisi sama panjang dan sepasang-sepasang sejajar.
b. sudut-sudut yang berhadapan sama besar dan terbagi dua sama besar.
Pada belah ketupat ABCD diatas, diketahui bahwa AB = BC = CD = AD = 6 cm,
Sudut A = sudut C = 400, dan sudut B = sudut D = 1400 (sudut-sudut yang berhadapan)
Pada belah ketupat EFGH diatas, diketahui bahwa EF = FG = GH = EH = 6 cm,
Sudut E = sudut G = 400, dan sudut F = sudut H = 1400
Dari uraian tersebut sanggup diperoleh:
AB/EF = BC/FG = CD/GF = AD=EH = 1
sudut A = sudut C = Sudut E = sudut G = 400
sudut B = sudut D = sudut F = sudut H = 1400
Karena sisi-sisinya yang bersesuaian mempunyai ukuran sama panjang serta sudut-sudut yang bersesuaian sama besarnya, maka berdiri ABCD dan EFGH bisa dikatakan kongruen.
Demikianlah materi kita hari ini, semoga bisa dipahami oleh anak anak semuanya, seandainya ada yang belum paham silahkan bertanya lewat WA.
LATIHAN
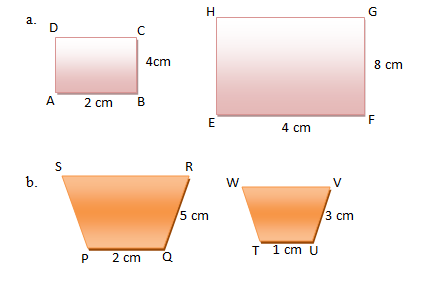
1. Apakah masing-masing pasangan bangun di bawah ini sebangun?
2. Perhatikan gambar berikut:
Trapesium ABCD dan PQRS sebangun, tentukanlah:
a. Panjang BC
b. Panjang RS
3. a. Apakah persegi panjang KLMN sebangun dengan persegi panjang PQRS?
b. Apakah persegi panjang KLMN kongruen dengan persegi panjang PQRS?
KESIMPULAN
Demikianlah materi hari ini semoga bisa di pahami dan kalau ada yang belum paham bisa bertanya langsung ke ibu ya nak.










Tidak ada komentar:
Posting Komentar