MATA PELAJARAN : MATEMATIKA
FASE : D
MATERI POKOK : PERSAMAAN LINIER DUA VARIABEL
PERTEMUAN : KE 1 DARI 4
GURU PENGAMPU : SARI BUDI UTAMI, S.Pd
CAPAIAN PEMBELAJARAN
Di akhir fase D Peserta didik dapat menyatakan suatu situasi ke dalam bentuk aljabar; operasi bentuk aljabar yang ekuivalen; menyelesaikan persamaan dan pertidaksamaan linear dengan dua variabel;
Tujuan Pembelajaran :
Setelah mengukuti kegiatan pembelajaran menggunakan model pembelajaran discovery Learning, dengan metode literasi, eksperimen, praktikum, dan presentasi dengan menumbuhkan sikap
1 . Beriman dan bertakwa kepada Tuhan yang maha Esa
2. Bergotong royong
3. Berkebinekaan global
Maka peserta didik Diharapkan dapat :
Assalamualaikum anak- anak yang sholeh sholehah....
Apa kabarnya hari ini ?
Semoga kita semua dalam lindungan Allah SWT Aamiin.....
Dan jangan lupa tetap selalu menjaga kesehatan nya ya nak.
Baiklah sebelum kita melaksanakan pembelajaran di pagi ini, alangkah baiknya kita awali dengan melaksanakan sholat dhuha dan murojaahnya terlebih dahulu ya nak, dan tak lupa setelah itu pembacaan asmaul husna dan doa belajar ya supaya ilmu yang dipelajari hari ini akan bermanfaat, mudah diterima dan akan berkah ilmunya
Sistem persamaan linear dua variabel bisa digunakan untuk menentukan harga barang, mencari keuntungan penjualan, dan lainnya.
Berdasarkan buku Ayo, Belajar Persamaan, Pertidaksamaan, dan Sistem Persamaan Linear! karya Mirna Indrianti, ada tiga cara yang biasa digunakan untuk menyelesaikan permasalahan persamaan linear dua variabel, yaitu menggunakan metode grafik, substitusi, dan eliminasi.
Metode Grafik
Metode ini menyelesaikan masalah dengan menentukan titik perpotongan dua garis lurus yang merupakan tampilan dari kedua persamaan linear dua variabel.
Berikut ini adalah langkah-langkah penyelesaian SPLDV dengan metode grafik:
1. Tentukan titik potong salah satu persamaan linear dengan sumbu X atau sumbu Y.
2. Hubungkan kedua titik potong dengan menggunakan garis lurus.
3. Lakukan langkah 1 dan 2 untuk persamaan lain pada SPLDV.
4. Jika kedua titik berpotongan di (x,y) = (x1, y1), penyelesaian SPLD adalah x=x1 dan y=y1.
5. Jika kedua titik tidak berpotongan, SPLDV tidak memiliki penyelesaian.
Contoh Soal
Tentukan penyelesaian dari sistem persamaan linear dua variabel berikut menggunakan metode grafik.
Penyelesaian
Tentukan titik perpotongan tiap-tiap persamaan terhadap sumbu X dan Y.
Untuk 4x + 5y = 40
Titik perpotongan terhadap sumbu X (y=0)
= 4x + 5(0) = 40
= 4x + 0 = 40
=x = 40/4 = 10
Jadi, garis berpotongan dengan sumbu X di (10,0)
Titik perpotongan terhadap sumbu Y (x=0)
= 4(0) + 5y = 40
= 0 + 5y = 40
=y= 40/5= 8
Jadi, garis berpotongan dengan sumbu Y di (0,8)
Untuk x + 2y = 14
• Titik perpotongan terhadap sumbu X (y=0)
= x + 2(0) = 14
= x + 0 = 14
= x = 14
Jadi, garis berpotongan dengan sumbu X di (14,0)
• Titik perpotongan dengan sumbu Y (x=0)
= 0 + 2y =14
= 2y = 14
= y = 14/2 = 7
Jadi, garis berpotongan terhadap sumbu Y di (0,7)
2. Gambarkan tiap-tiap persamaan dalam sebuah koordinat Kartesius.
3. Jika sudah Digambar, kalian akan mendapat perpotongan di titik (x,y) = (2,6)
LATIHAN
1. Diketahui pada persamaan x + 3y = 15 dan 3x + 6y = 30, Dengan menggunakan cara metode grafik tentukanlah himpunan penyelesaiannya !
KESIMPULAN
Demikianlah materi hari ini yaitu tenyang penyelesaian persamaan kuadrat dengan menggunakan metode grafik.
Berikut ini adalah langkah-langkah penyelesaian SPLDV dengan metode grafik:
1. Tentukan titik potong salah satu persamaan linear dengan sumbu X atau sumbu Y.
2. Hubungkan kedua titik potong dengan menggunakan garis lurus.
3. Lakukan langkah 1 dan 2 untuk persamaan lain pada SPLDV.
4. Jika kedua titik berpotongan di (x,y) = (x1, y1), penyelesaian SPLD adalah x=x1 dan y=y1.
5. Jika kedua titik tidak berpotongan, SPLDV tidak memiliki penyelesaian.
REVFERENSI
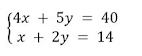
Tidak ada komentar:
Posting Komentar