Hari/ Tanggal : Selasa dan Jumat, 2 dan 5 Agustus 2022
Kelas : 8A
Materi : Pola Bilangan
KOMPETENSI DASAR
3.1 Membuat generalisasi dari pola pada barisan bilangan dan barisan
konfigurasi objek.
4.1 Menyelesaikan masalah yang berkaitan dengan pola pada barisan bilangan.
Tujuan Pembelajaran :
Setelah mengukuti kegiatan pembelajaran menggunakan model pembelajaran discovery Learning, dengan metode literasi, eksperimen, praktikum, dan presentasi dengan menumbuhkan sikap menyadari kebesaran Tuhan, sikap gotong royong, jujur, dan berani mengemukakan pendapat, siswa dapat :
· Menjelaskan salah satu konfigurasi objek yang terkait dengan pola bilangan
· Mengidentifikasi pola bilangan dari suatu barisan
Assalamualaikum anak- anak yang sholeh sholehah....
Apa kabarnya hari ini ?
Semoga kita semua dalam lindungan Allah SWT Aamiin.....
Dan jangan lupa tetap selalu menjaga kesehatan dan selalu memakai prokes nya ya nak.
Baiklah sebelum kita melaksanakan pembelajaran di pagi ini, alangkah baiknya kita awali dengan melaksanakan sholat dhuha dan murojaahnya terlebih dahulu ya nak, dan tak lupa setelah itu pembacaan asmaul husna dan doa belajar ya supaya ilmu yang dipelajari hari ini akan bermanfaat, mudah diterima dan akan berkah ilmunya
Baiklah untuk pertemuan kali ini kita akan memasuki materi
B. Barisan Sebagai Suatu Fungsi
Untuk menentukan suku-suku suatu barisan, dapat dilihat dari keteraturan pola dari suku
– suku sebelumnya. Salah satu cara untuk menentukan rumus umum suku ke-n suatu
barisan adalah dengan memperhatikan selisih antara dua suku yang berurutan. Bila pada
satu tingkat pengerjaan belum diperoleh selisih tetap, maka pengerjaan dilakukan pada
tingkat berikutnya sampai diperoleh selisih tetap. Suatu barisan disebut berderajat satu
bila selisih tetap diperoleh dalam satu tingkat pengerjaan, disebut berderajat dua bila
selisih tetap diperoleh dalam dua tingkat pengerjaan dan seterusnya.
Untuk memahami pengertian barisan berderajat satu, berderajat dua, dan seterusnya
perhatikan contoh berikut:
Barisan 2, 5, 8, 11, … disebut barisan berderajat satu karena selisih tetap diperoleh
pada satu tingkat penyelidikan.
Barisan 5, 8, 13, 20, 29, … disebut barisan berderajat dua karena selisih tetap
diperoleh pada dua tingkat penyelidikan.
Untuk menentukan rumus suku ke-n masing-masing barisan itu dilakukan dengan cara
sebagai berikut:
1. Barisan linier berderajat satu
Karena barisannya berderajat satu maka bentuk umum suku ke – n adalah Un = an + b,
sehingga
U1 = a + b,
U2 = 2a + b,
U3= 3a + b, dan seterusnya.
Dengan demikian rumus umum suku ke – n barisan 2, 5, 8, 11, ... dapat ditentukan
dengan cara:
Jadi rumus suku ke – n barisan 2, 5, 8, 11, ... adalah Un= 3n – 1
2. Barisan linier berderajat dua
Karena barisannya berderajat satu maka bentuk umum suku ke – n adalah Un +bn + c.
Dengan demikian
U1 = a + b + c,
U2 = 4a + 2b + c,
U3= 9a + 3b + c,
danseterusnya.
Dengan demikian rumus umum suku ke – n barisan 5, 8, 13, 20, 29, … dapat
ditentukan dengan cara :
Jadi rumus suku ke – n barisan 5, 8, 13, 20, 29, … adalah Un= n 2+ 4
Latihan Soal
Kerjakan soal dibawah ini dengan benar dan jelas.
1. Tentukan dan susun 5 bilangan pertama yang memenuhi aturan / pola sebagai berikut,
untuk n bilangan Asli:
a. 2n – 3
b. 2n + n2
c. 1/2n + 1
d. (n – 1)2
e. 5n + 2(n2 – 1)
2. Carilah dua suku berikutnya dari barisan bilangan
a. 4, 6, 9, 13, 18, …, …
b. 4, 7, 10, 13, ..., ...
3. Andi diberi tugas oleh Pak Marno untuk meletakkan buku di rak perpustakaan. Di rak
pertama ia harus meletakkan 6 buah buku, di rak kedua 11 buah buku, di rak ketiga 16
buah buku, di rak keempat 21 buah buku. Jika banyaknya rak di perpustakaan adalah 10,
tentukan banyaknya buku yang harus disusun Budi di rak terakhir!



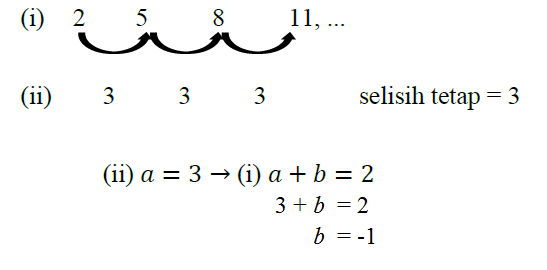


Tidak ada komentar:
Posting Komentar