SEGITIGA - SEGITIGA KONGRUEN

  SEGITIGA - SEGITIGA KONGRUEN

  HARI/TANGGAL  :  KAMIS / 21 JANUARI 2021

  KELAS                    : 9F, 9G

  KD                           : 3.6 Menjelaskan dan menentukan kesebangunan dan kekongruenan antar  

                                     bangun  datar

  TUJUAN                 : Setelah mengikuti proses pembelajaran, peserta didik dapat:

·                                         Menentukan kesebangunan dan kekongruenan segitiga-segitiga yang kongruen

Selamat pagi anak sholeh dan sholeha?  

Semoga kalian selalu menjaga kesehatan dan rajin berolahraga ya nak agar tubuh kita sehat dan tidak mudah terserang penyakit serta semoga kita semua selalu dalam lindungan allah swt amin ya rabbal alamin 

Baiklah sebelum kita melaksanakan postest hari ini, jangan lupa untuk melaksanakan sholat dhuha, murojaah pagi dan mendengarkan opening class, Serta dilanjutkan dengan pembacaan Asmaul Husna dan doa belajar ya. 

 Serta tak lupa untuk melaksanakan sholat 5 waktunya ya nak... 

Tetep semangat ya....

Kongruen dilambangkan dengan 

≅, sehingga jika terdapat dua buah segitiga yang kongruen misalnya ΔABC kongruen dengan ΔPQR, maka dapat ditulis sebagai ΔABC≅ΔPQR.

Perhatikan gambar berikut.

Dari gambar di atas diketahui bahwa ΔACM adalah segitiga sama kaki. Sisi AP merupakan garis tinggi ΔACM, sehingga membentuk ΔACP dan ΔAMP. Apakah ΔACP kongruen dengan ΔAMP? ΔACP kongruen dengan ΔAMP (ΔACP ≅ ΔAMP) karena:

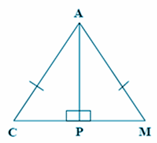
• ΔACP dapat tepat menempati ΔAMP dengan cara mencerminkan ΔACP terhadap garis AP atau semua sisi ΔACP memiliki panjang yang sama dengan ΔAMP.
• ΔCAM merupakan segitiga sama kaki, sehingga ∠ACP = ∠AMP (sudut pada kaki segitiga samakaki ΔCAM) dan ∠APC = ∠APM = 90⁰. Ini berakibat ∠CAP = ∠MAP.

Dari uraian di atas diperoleh kesimpulan sebagai berikut.

Sifat-Sifat Dua Segitiga yang Kongruen

• Sisi–sisi yang bersesuaian mempunyai panjang yang sama
• Sudut–sudut yang seletak besarnya sama

Segitiga dapat dikatakan kongruen mana kala dapat memenuhi syarat yskni sebagai berikut:

a. Tiga Sisi yang Bersesuaian Sama Besar (sisi, sisi, sisi)

Berdasarkan gambar dari segitiga ABC serta segitiga PQR di atas, diketahui jika keduanya mempunyai panjang AB = PQ, panjang AC = PR, serta panjang BC = QR. 

b. Sudut dan Dua Sisi yang Bersesuaian Sama Besar (sisi, sudut, sisi)

Berdasarkan dari gambar bangun segitiga ABC serta segitiga PQR di atas, diketahui jika kedua bangunnya memiliki sisi AB = PQ, ∠B = ∠Q, dan juga sisi BC = QR

c. Satu Sisi Apit dan Dua Sudut yang Bersesuaian Sama Besar (sudut, sisi, sudut)

Berdasarkan dari gambar bangun segitiga ABC dan segitiga PQR di atas, diketahui bahwa, ∠A = ∠P, sisi AC = PR, serta ∠Q = ∠R.

Contoh 1

Perhatikan gambar berikut.

Jika ΔABC kongruen dengan ΔPQR, maka tentukan:
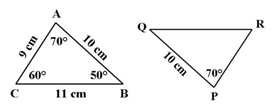
- panjang PR
- panjang QR
- ∠PQR
- ∠QRP

Penyelesaian:

• Oleh karena sisi PR bersesuaian dengan AC, maka panjang sisi PR = AC = 9 cm.
• Oleh karena sisi QR bersesuaian dengan CB, maka panjang QR = CB = 11 cm.
• Oleh karena ∠PQR bersesuaian dengan ∠ABC, maka ∠PQR = ∠ABC = 50⁰.
• Oleh karena ∠QRP bersesuaian dengan ∠ACB, maka ∠ QRP = ∠ ACB = 60⁰.

Perbedaan antara Kesebangunan dan Kekongruenan pada Segitiga

DEMIKIANLAH MATERI HARI INI, SEMOGA BERMANFAAT BUAT KALIAN. KALAU MASIH

 ADA YANG BELUM PAHAM SILAHKAN BERTANYA LEWAT WA.

UNTUK LATIHAN MANDIRI SILAHKAN KERJAKAN LATIHAN 5 BUKU PAKET 3B

 HAL. 22    NO 1,2,3,4,5.

KIRIMKAN KE EMAIL IBU

TERIMA KASIH