KESEBANGUNAN & KEKONGRUENAN

HARI/TANGGAL  : KAMIS/7JANUARI 2021

KELAS                    : 9F & 9G

KD                           : 3.6 Menjelaskan dan menentukan kesebangunan dan kekongruenan antar bangun datar

TUJUAN                        : Setelah mengikuti proses pembelajaran, peserta didik dapat:

·                                                                    Menjelaskan Kesebangunan dua bangun datar

Pengertian Kesebangunan Bangun Datar

Kesebangunan merupakan sebuah bangun datar di mana sudut – sudutnya mempuntai kesesuaian yang sama besarnya. Dan juga panjang sisi – sisi sudutnya juga bersesuai dengan mempunyai sebuah perbandingan yang sama.

Perhatikan contoh di bawah ini:

Dua Bangun Datar yang Sebangun

Sekarang, coba kamu perhatikan Gambar di atas! Sebangunkah persegipanjan ABCD dengan persegipanjang EFGH? Pada persegipanjang ABCD dan persegipanjang EFGH, perbandingan panjangnya adalah 4 : 8 = 1 : 2.

Adapun perbandingan lebarnya adalah 2 : 4 = 1 : 2. Dengan demikian, perbandingan sisi-sisi yang bersesuaian pada kedua persegipanjang tersebut dapat dinyatakan sebagai berikut.

Dua bangun datar yang sebangun

Kedua bangun di atas, ABCD dan KLMN  adalah dua bangun yang sebangun, karena memiliki sifat-sifat sebagai berikut :

a.       Pasangan sisi yang bersesuaian mempunyai perbandingan yang sama, yaitu
:

Pasangan sisi AD dan KN =  

Pasangan sisi AB dan KL = 

Pasangan sisi BC dan LM =   

Pasangan sisi CD dan MN = 

Jadi,   

b.      Besar sudut yang bersesuaian sama, yaitu :

Kemudian, perhatikan sudut-sudut yang bersesuaian pada persegipanjang ABCD dan persegipanjang KLMN. Oleh karena keduanya berbentuk persegipanjang, setiap sudut besarnya 90° sehingga sudut-sudut yang bersesuaian pada kedua bangun tersebut sama besar.

Pengertian Kekongruenan

Kekongruenan merupakan dua buah bangun datar yang di mana kedua bangunnya sama – sama memiliki bentuk dan juga ukuran yang sama.

Kekongruenan ini biasa dilambangkan dengan pemakaian simbol ≅.

Perhatikan contoh di bawah ini:

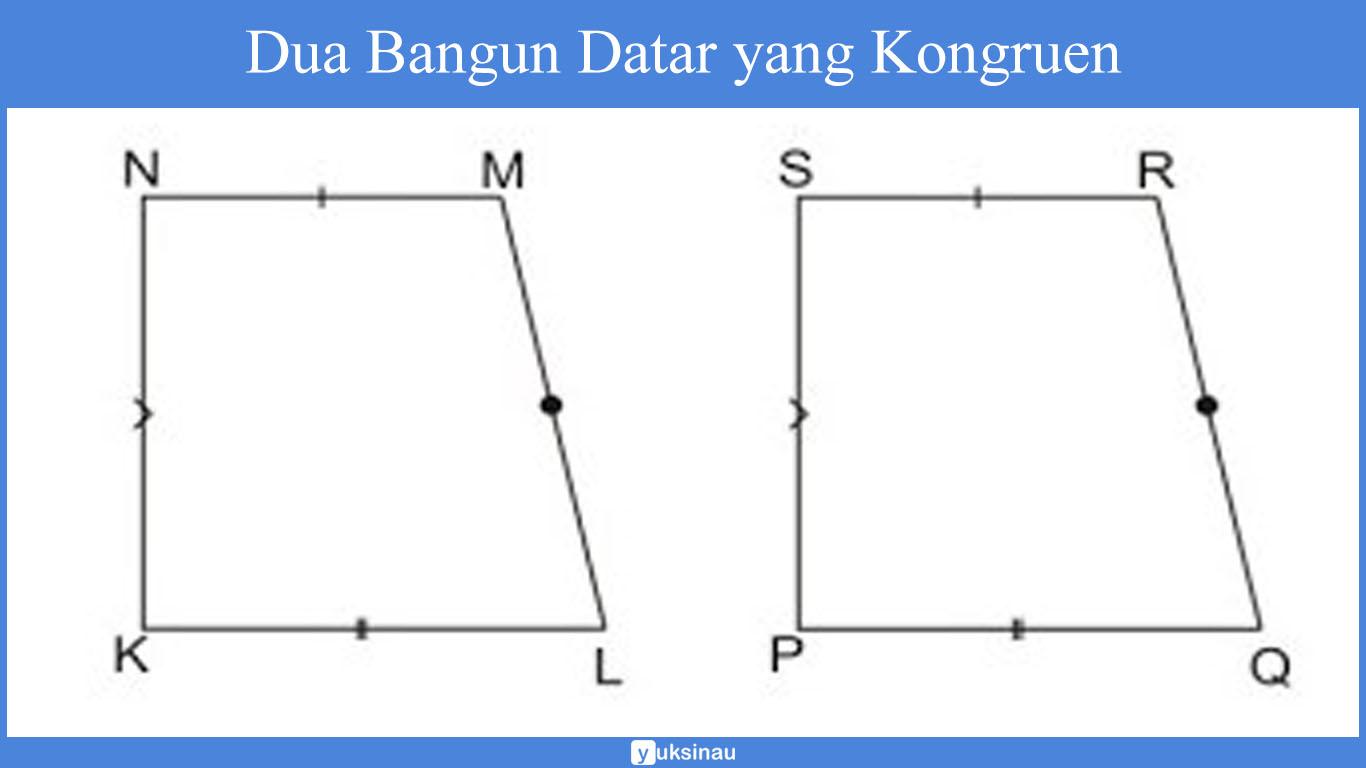
1. Dua Bangun Datar yang Kongruen

Pada kedua bangun di atas adalah bangun yang kongruen, karena panjang KL = PQ, Panjang LM = QR, panjang MN = RS, panjang NK = SP maka oleh karena itu, pada bangun KLMN dan PQRS dapat dikatakan adalah kongruen karena memiliki bentuk dan ukuran yang sama.

Perbedaan Kesebangunan dan Kekongruenan

Hal mendasar yang membedakan kongruen dan sebangun yaitu:

Bangun dikatakan kongruen jika sisi-sisi yang bersesuaian harus sama panjang. Sementaa jika bangun dikatakan sebangun apabila perbandingan sisi-sisi yang bersesuaian harus sama besar.

Sehingga dapat kita simpulkan bahwa, seluruh bangun yang kongruen sudah pasti sebangun, namun jika sebangun belum tentu kongruen.