FUNGSI

 MATA PELAJARAN            : MATEMATIKA

 FASE                                     :  D

MATERI POKOK                 : RELASI DAN FUNGSI

PERTEMUAN                       : KE 3 DARI 4

GURU PENGAMPU             : SARI BUDI UTAMI, S.Pd

CAPAIAN PEMBELAJARAN

Di akhir fase D Peserta didik dapat memahami relasi dan fungsi (domain,kodomain, range) dan menyajikannya dalam bentukdiagram panah, tabel, himpunan pasangan berurutan,dan grafik. Mereka dapat membedakan beberapa fungsinonlinear dari fungsi linear secara grafik. 

Tujuan Pembelajaran :

Setelah mengukuti kegiatan pembelajaran menggunakan model pembelajaran discovery Learning, dengan metode literasi, eksperimen, praktikum, dan presentasi dengan menumbuhkan sikap

 1 .  Beriman dan bertakwa kepada Tuhan yang maha Esa

2.      Bergotong royong

3.      Berkebinekaan global

Maka peserta didik Diharapkan dapat :

1.  Menjelaskan dengan kata- kata dan menyatakan masalah sehari-hari yang berkaitan  dengan fungsi.

2. Mendefinisikan fungsi

3.  Mengamati fungsi dan bukan fungsi

•   

Assalamualaikum anak- anak yang sholeh sholehah....

Apa kabarnya hari ini ?

Semoga kita semua dalam lindungan Allah SWT Aamiin.....

Dan jangan lupa tetap selalu menjaga kesehatan  nya ya nak.

Baiklah sebelum kita melaksanakan pembelajaran di pagi ini, alangkah baiknya kita awali dengan melaksanakan sholat dhuha dan murojaahnya terlebih dahulu ya nak, dan tak lupa setelah itu pembacaan asmaul husna dan doa belajar ya supaya ilmu yang dipelajari hari ini akan bermanfaat, mudah diterima dan akan berkah ilmunya 

Sebelum kita membahas materi minggu ini masih ingatkah kalian dengan materi minggu kemarin.......?Iya materi minggu kemarin yaitu tentang Relasi. Sekilas kita ulang materi minggu lalu tentang Relasi yaitu hubungan antara dua himpunan.

Baiklah pada pertemuan  ini, materi yang akan kita pelajari adalah tentang Fungsi

 Fungsi (Pemetaan)

1. Pengertian Fungsi (pemetaan)
Fungsi dari himpunan A ke himpunan B merupakan relasi yang menghubungkan setiap anggota himpunan A ke tepat satu anggota himpunan B.

Selain fungsi dikenal juga istilah pemetaan. Keduanya memiliki makna yang sama. Perhatikan ilustrasi di bawah ini:

Contoh Pemetaan/Fungsi:

Dari gambar di atas terdapat dua himpunan yaitu himpunan P ={Ali, Budi, Cahrlie, Donie, Eka} dan himpunan Q ={A,B,O,AB}. Setiap orang dalam himpunan P dipasangkan tepat dengan satu golongan darah yang merupakan anggota himpunan Q. Bentuk relasi yang seperti inilah yang disebut dengan fungsi. Jadi definisi fungsi atau pemetaan adalah

“Fungsi atau pemetaan adalah hubungan atau relasi spesifik yang memasangkat setiap anggota suatu himpunan dengan tepat satu anggota himpunan yang lain.”

Domain, Kodomain, dan Range Fungsi

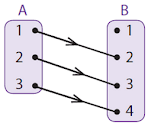
Dalam materi fungsi dikenal istilah Domain, Kodomain, dan juga Range Fungsi. Coba sobat perhatikan gambar di bawah ini.

Dari diagram panah tersebut himpunan A atau himpunan daerah asal disebut dengan Domain. Himpunan B yang merupakan daerah kawan disebut dengan Kodomain sedangkan anggota daerah kawan yang merupakan hasil dari pemetaan disebut dengan daerah hasil atau range fungsi. Jadi dari diagram panah di atas dapat disimpulkan

Domain (D_f) adalah A = {1,2,3}
Kodomain adalah B = {1,2,3,4}
Range Hasil (R_f) adalah = {2,3,4}

Grafik Fungsi

Grafi fungsi adalah grafik yang menggambarkan bentuk suatu fungsi dalam diagram cartesius. Grafik ini diperoleh dengan menghubungkan noktah-noktah yang merupakan pasangan berurutan antara daerah asal (sumbu x) dan daerah hasil (sumbu y).

Menghitung Nilai dari Sebuah Fungsi

1. Notasi Fungsi

Sebuah fungsi dinotasikan dengan huruf kecil seperti f, g, h, i, dan sebagainya. Pada fungsi g yang memetakan himpunan A ke himpunan B dinotasikan dengan g(x). Misal ada fungsi f yang memetakan A ke B dengan aturan f : x → 2x + 2. Dari notasi fungsi tersebut, x merupakan anggota domain. fungsi x → 2x + 2 berarit fungsi f memetakan x ke 2x+2. Jadi daerah bayangan x oleh fungsi f adalah 2x + 2. Sobat dapat menotasikannya dengan f(x) = 2x +2. Kesimpulan

Jika fungsi f : x → ax + b dengan x anggota domain f maka rumus fungsi f adalah f(x) = ax +b

2. Menghitung nilai dari Sebuah Fungsi

Menghitung nilai dari sebuah fungsi cukup sederhana. Sobat hanya perlu mengikuti rules dari fungsi tersebut. Semakin susah fungsi yang memetakannya maka akan semakin susah menghitung nilai fungsinya. Terkadang soal-soal membalik fungsi tersebut, diketahui daerah hasil kemudian diminta mencari daerah asal. Yuk mari dismak contoh berikut:

Diketahui fungsi f : x → 2x – 2 dengan x anggota bilangan bulat. Coba sobat tentukan nilai dari

1. f(3)
2. f(4)
3. bayangan (-3) oleh f
4. nilai f untuk x = -10
5. nilai a jika f(a) = 14

Jawaban
fungsi fungsi f : x → 2x – 2 dapat dinyatakan dengan f(x) = 2x – 2

1. f(x) = 2x – 2
   f(1) = 2(3) – 2 = 4
2. f(x) = 2x – 2
   f (4) = 2(4) – 2 = 6
3. f(x) = 2x – 2
   f(-3) = 2(-3) – 2 = -8
4. f(x) = 2x – 2
   f(10) = 2(10) -2 = 18
5. f(a) = 2a – 2
   14 = 2a -2
   2a = 16
   a = 8

3. Menentukan Rumus sebuah fungsi

Sebuah fungsi dapat sobat temukan rumusnya apabila ada nilai atau data yang diketehui. Kemudian dengan menggunakan aljabar sobat bisa dengan mudah menemukan rumus dari fungsi tersebut. Untuk lebih jelasnya bisa sobat simak contoh berikut:

Fungsi g yang berlaku pada himpunan bilangan riil ditentukan oleh rumus g(x) = ax + b dengan a dan b adalah bilangan bulat. Jika g(-2) = -4 dan g(1) = 5. Coba sobat tentukan nalai dari:

1. nilai dari a dan b
2. rumus fungsi
3. g (-3)

Jawaban

1. Untuk mencari nila a dan b kita buat persamaan dulu dari himpunan pasangan berurutan yang diketahui.
   g(-2) = -4 → -4 = -2a + b → b = 2a – 4 _…(1)
   g(1) = 5    →  5 = a + b _…(2)
   kita substitusikan persamaan 1 ke persamaan 2

5 5 5 9 a

= a + b = a + 2a – 4 = 3a – 4 = 3a = 3

2. b = 2a – 4
   b = 2(3) -4
   b = 2
   jadi nilai a = 3 dan b = 4
3. rumus fungsinya g(x) = 3a + 2
4. g(x) = 3a + 2
   g(-3) = 3 (-3) + 2
   g (-3) = -7

LATIHAN

1. Diberikan relasi R  dari himpunan A = (1, 2, 3, 4)  ke himpunan B = (a, b, c, d)  dengan aturan R = (1, a), (2, b), (3, c), (4, d)) . Berapakah banyaknya unsur dalam R ?  

2. Diberikan himpunan X = (1, 2, 3, 4)  dan himpunan Y = (a, b, c). Jika terdapat relasi R  dari X  ke Y  yang memenuhi syarat bahwa setiap elemen dalam X  terhubung dengan setiap elemen dalam Y , maka R  merupakan … 

3. Diberikan relasi R  dari himpunan A = (a, b, c)  ke himpunan B = (1, 2, 3)  dengan aturan R = (a, 1), (b, 2), (c, 3) . Himpunan bagian dari A  yang memiliki elemen yang terhubung dengan 2  adalah …  

4. Diketahui

P = (bilangan kelipatan 7 kurang dari 24)

Q = (bilangan prima kurang dari 11)

Banyaknya pemetaan yang mungkin dari P ke Q adalah ... .

KESIMPULAN

Demikianlah materi kita hari ini tentang Fungsi, jadi Fungsi itu adalah relasi khusus yang memasangkan anggota himpunan A tepat satu dengan anggota himpunan B.

Banyaknya Fungsi atau pemetaan dari himpunan A ke himpunan B dengan menggunakan rumus n(B) dipangkatkan n(A).

Reverensi

https://mamikos.com/info/contoh-soal-relasi-dan-fungsi-pljr/

https://kumparan.com/berita-terkini/6-contoh-soal-relasi-dan-fungsi-kelas-8-lengkap-dengan-pembahasannya-1ynciRhoTpH