FUNGSI

  Hari/ Tanggal : Selasa dan Jumat, 11 dan  14 Oktober  2022

 Kelas              : 8A 

 Materi            :  Relasi dan Fungsi

KOMPETENSI DASAR

3.3   Mendeskripsikan dan manyatakan relasi dan fungsi dengan menggunakan berbagai representasi (kata-kata, tabel, grafik, diagram, dan persamaan)

4.3   Menyelesaikan masalah yang berkaitan dengan relasi dan fungsi dengan menggunakan berbagai representasi

Tujuan Pembelajaran :

Setelah mengukuti kegiatan pembelajaran menggunakan model pembelajaran discovery Learning, dengan metode literasi, eksperimen, praktikum, dan presentasi dengan menumbuhkan sikap menyadari kebesaran Tuhan, sikap gotong royong, jujur, dan berani mengemukakan pendapat, siswa dapat :

• Menjelaskan macam-macam fungsi berdasarkan ciri-cirinya

• Menjelaskan nilai fungsi dan grafik fungsi pada koordinat Kartesius

• Menyajikan hasil pembelajaran relasi dan fungsi

 

Assalamualaikum anak- anak yang sholeh sholehah....

Apa kabarnya hari ini ?

Semoga kita semua dalam lindungan Allah SWT Aamiin.....

Dan jangan lupa tetap selalu menjaga kesehatan dan selalu memakai prokes nya ya nak.

Baiklah sebelum kita melaksanakan pembelajaran di pagi ini, alangkah baiknya kita awali dengan melaksanakan sholat dhuha dan murojaahnya terlebih dahulu ya nak, dan tak lupa setelah itu pembacaan asmaul husna dan doa belajar ya supaya ilmu yang dipelajari hari ini akan bermanfaat, mudah diterima dan akan berkah ilmunya 

Baiklah untuk pertemuan kali ini kita akan memasuki materi 

Definisi Fungsi

Fungsi (pemetaan) merupakan relasi dari himpunan A ke himpunan B, jika setiap anggota himpunan A berpasangan tepat satu dengan anggota himpunan B. Semua anggota himpunan A atau daerah asal disebut domain, sedangkan semua anggota himpunan B atau daerah kawan disebut kodomain. Hasil dari pemetaan antara domain dan kodomain disebut range fungsi atau daerah hasil.

Cara Menyatakan Fungsi

Sama halnya dengan relasi, fungsi juga dapat dinyatakan dalam bentuk diagram panah, himpunan pasangan berurutan dan dengan diagram Cartesius.

Contoh:

Jadi, dari diagram panah di atas dapat disimpukan:

Domain adalah A = {1,2,3}

Kodomain adalah B = {1,2,3,4}

Range fungsi = {2,3,4}

 

Notasi Fungsi

Sebuah fungsi dapat dinotasikan dengan huruf kecil sepeti f, g, h. Misal, fungsi f memetakan himpunan A ke himpunan B dinotasikan f(x) dengan aturan f : x → 3x+3. Artinya fungsi f memetakan x ke 3x+3. Jadi daerah bayangan x oleh fungsi f adalah 3x+3 sehingga dapat dinotasikan dengan f(x) = 3x+3. Dari uraian ini dapat dirumuskan:

Jika fungsi f : x → ax +b dengan x anggota domain f , maka rumus fungsif adalah f(x) = ax+b

Dengan menghitung nilai fungsi, kita dapat mengetahui nilai fungsi yang dapat menghasilkan himpunan kawan (kodomain) dari himpunan asal (domain). Supaya lebih jelas, coba kerjakan contoh soal di bawah ini ya.

Diketahui fungsi f : x → 3x + 3 pada himpunan bilangan bulat. Tentukan:

f(3)

bayangan (-2) oleh f

nilai f untuk x = -4

nilai x untuk f(x) = 6

nilai a jika f(a) = 12

Jawab:

Fungsi f : x → 3x + 3

Rumus fungsi: f(x) = 3x+3

f(3) = 3(3)+3 = 12

bayangan (-2) oleh f sama dengan f (-2), jadi f(-2) = 3(-2)+3 = -3

nilai f untuk x = -4 adalah f (-4) = 3(-4)+3 = -9

nilai x untuk f(x) = 6 adalah

3x + 3 = 6

3x = 6-3

3x = 3

x = 1

5. nilai a jika f(a) = 12

3a + 3 = 12

3a = 12 – 3

3a = 9

a = 3

CONTOH SOAL

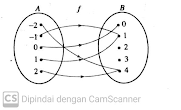
Diagram di atas menunjukkan pemetaan (fungsi) f dari himpunan A ke B. Tentukan:

a. Daerah asal (domain)

b. Daerah kawan (kodomain)

c. Daerah hasil (range)

Jawaban:

Kita akan menjawabnya satu per satu.

a. Daerah asal atau domain

A = {-2, -1, 0, 1, 2} disebut daerah asal. Jika dilihat pada diagram panah biasanya terletak di sebelah kiri.

b. Daerah kawan atau kodomain

B = {0, 1, 2, 3, 4} disebut daerah kawan. Pada diagram panah letaknya di bagian kanan.

c. Daerah hasil atau range

Daerah hasilnya adalah {0, 1, 4}. Daerah hasil yaitu himpunan anggota-anggota B yang mempunyai pasangan dengan anggota-anggota P.

LATIHAN

1. Sebuah pemetaan dinytakan dalam bentuk R = {(1,a), (2,b), (3,a), (4,b)}. Tentukan domain, kodomain dan rangenya…

2. Diketahui M={2, 3, 4, 5, 6} dan N={a,b}. Relasi R memasangkan setiap bilangan genap pada M dengan a dan setiap bilangan ganjil pada M dengan b.

a. Nyatakan R dengan diagram panah

b. Apakah R merupakan pemetaan dari M ke N

3. Diketahui  A = {bilangan ganjil kurang dari 8} dan B = {bilangan prima genap}.  Banyak pemetaan dari B ke A adalah…

4. Buatlah empat diagram panah yang berlainan untuk korespondensi satu-satu antara himpunan A = {a, b, c, d} dan B={1, 2, 3, 4}

5.a. Buatlah tabel fungsi f : x → x + 1 dari himpunan {0, 1, 2, 3} ke himpunan bilangan bulat.

   b. Gambarlah grafik fungsi f tersebut.

   c. Pada gambar yang sama, gambarlah grafik fungsi x → x + 1 pada himpunan semua bilangan positif dan nol.