MATA PELAJARAN : MATEMATIKA
KELAS : IX C, D
GURU PENGAMPU : SARI BUDI UTAMI, S.Pd.
WAKTU PEMBELAJARAN : 18 MARET 2024
KOMPETENSI DASAR :
3.7 Membuat generalisasi luas permukaan dan volume berbagai bangun ruang sisi lengkung (tabung, kerucut, dan bola)
TUJUAN PEMBELAJARAN :
Setelah mengikuti proses pembelajaran ini pesertadidik diharapkan dapat menyebutkan unsur, sifat sifat serta membuat generalisasi luas permukaan bangun ruang sisi lengkung (tabung) sampai benar.
Pengertian Bangun Ruang Sisi Lengkung
KERUCUT
Pengertian Kerucut
Kerucut merupakan salah satu bangun ruang yang memiliki sebuah alas yang berbentuk lingkaran dengan selimut yang mempunyai irisan dari lingkaran.
Di dalam geometri, kerucut merupakan sebuah limas istimewa yang memiliki alas lingkaran. Kerucut mempunyai 2 sisi dan 1 rusuk. Sisi tegak kerucut tidak berwujud segitiga namun berwujud bidang miring yang disebut sebagai selimut kerucut.
Yang membedakan antara limas dengan kerucut yaitu alas kerucut memiliki bentuk lingkaran, sementara pada limas berbentuk segi n beraturan.
Unsur-unsur Kerucut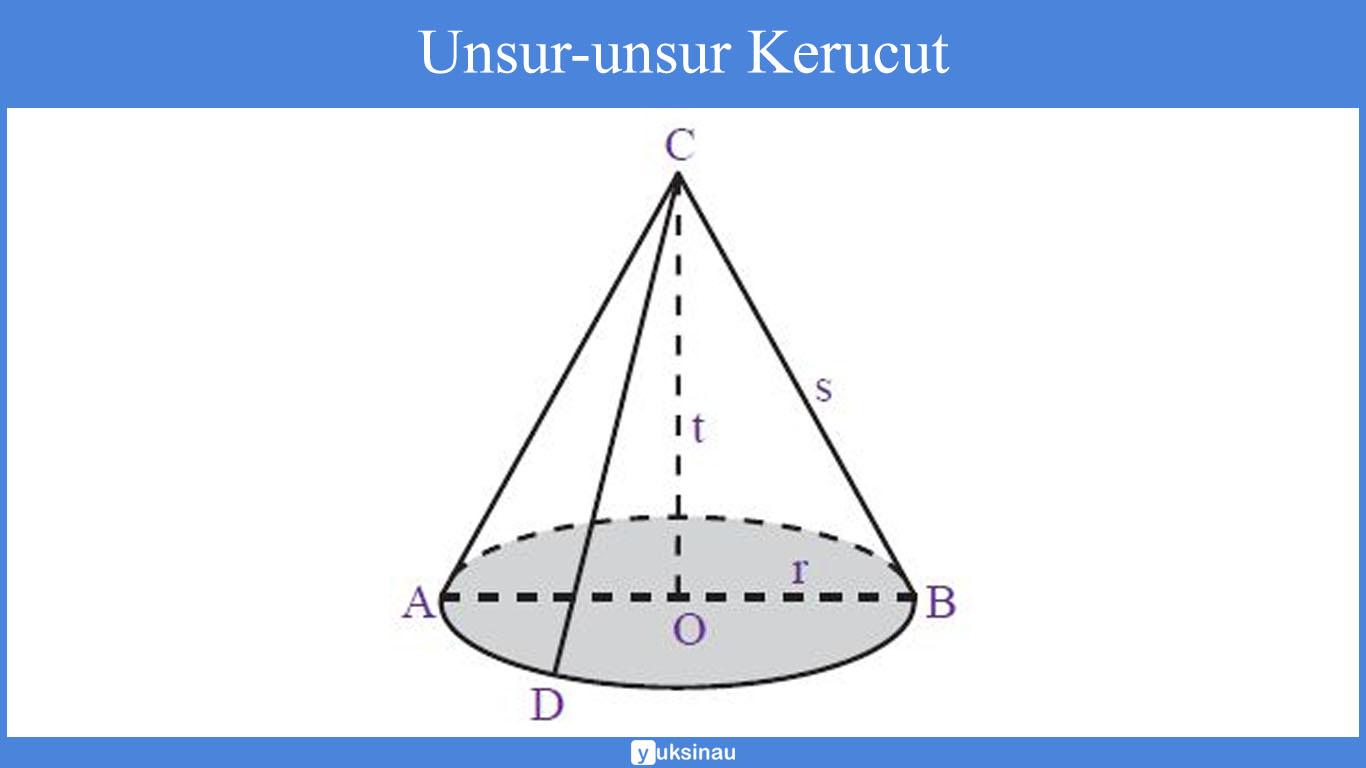
luas permukaan kerucut
1. Bidang alas, yakni sisi yang berbentuk lingkaran (daerah yang diraster).
2. Diameter bidang alas (d), merupakan ruas garis AB.
3. Jari-jari bidang alas (r), merupakan garis OA serta ruas garis OB.
4. Tinggi kerucut (t), yakni jarak dari titik puncak kerucut ke pusat bidang alas (ruas garis CO).
5. Selimut kerucut, merupakan sisi kerucut yang tidak diraster.
6. Garis pelukis (s), merupakan garis-garis pada selimut kerucut yang ditarik dari titik puncak C ke titik pada lingkaran.
s2 = r2 + t2 | r2 = s2 ─ t2 | t2 = s2 ─ r2 |
Sifat Kerucut
Terdapat beberapa sifat pada bangun ruang kerucut, antara lain ialah sebagai berikut:
1. Kerucut memiliki 2 sisi.
2. Kerucut tidak memiliki rusuk.
3. Kerucut memiliki 1 titik sudut.
4. Jaring-jaring kerucut terdiri atas lingkaran serta segitiga.
5. Tidak memiliki bidang diagonal
6. Tidak memiliki diagonal bidang
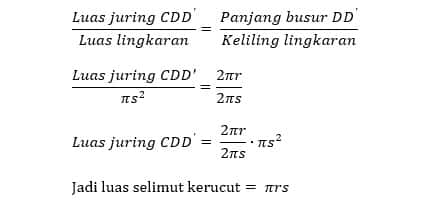
Rumus luas selimut kerucut
sama dengan luas juring CDD’.
Rumus Luas permukaan kerucut
= Luas selimut + Luas alas
dengan:
r : jari-jari lingkaran alas
s : apotema
π = 22/7 atau 3,14
Contoh Soal Luas Permukaan Kerucut :
Soal 1.
Panjang jari-jari alas sebuah kerucut adalah 7 cm serta tingginya 24 cm. Hitunglah luas seluruh kerucut itu dengan π = 22/7!
Penyelesaian :
Diket :
r = 7 cm
t = 24 cm
Dit : Luas seluruh kerucut?
Jawab :
Perhatikan gambar sebuah kerucut diatas, hubungan antara r,s dan t merupakan sebuah segitiga siku2 sehingga berlaku rumus phytagoras.
s² = r² + t²
s² = 7² + 24²
s² = 625
s = 25
Luas seluruh kerucut = πr² + πrs
Luas seluruh kerucut = πr(r+s)
Luas seluruh kerucut = 22/7×7×(7+25)
Luas seluruh kerucut = 22×32
Luas seluruh kerucut = 704 cm²
2. Diketahui volume kerucut besarnya 2.464 cm³. Jika diameter alas kerucutnya 28 cm, maka tentukan tinggi kerucut tersebut?
Jawaban.
Contoh soal kerucut ini dapat diselesaikan dengan cara seperti berikut:
V kerucut = 2.464 cm³
d = 28 cm
r = 14 cm
Volume kerucut = 1/3πr²t
2.464 = 1/3 x 22/7 x 14² x t
2.464 = 616/3 x t
t = 2.464 x 3/616
t = 12 cm
Jadi tinggi kerucut tersebut ialah 12 cm.
3. Diketahui jari jari kerucut 6 cm dan tinggi kerucut 8 cm. Tentukan luas permukaan kerucut tersebut?
Jawaban.
r = 6 cm
t = 8 cm
Contoh soal kerucut tersebut dapat diselesaikan dengan mencari panjang selimut kerucut terlebih dahulu. Adapun caranya yaitu:
s² = r² + t²
s² = 6² + 8²
s² = 36 + 64
s² = 100
s = 10 cm
Maka,
Luas permukaan kerucut = πr(r+s)
= 3,14 x 6 (6 + 10)
= 301,44 cm²
Jadi luas permukaan kerucut tersebut ialah 301,44 cm².
LATIHAN
a. 12
b. 14
c. 15
d. 16
2. Panjang diameter sebuah kerucut 28 cm. Jika tingginya 48 cm, maka luas seluruh kerucut tersebut adalah .... cm²
a. 2.786
b. 2.816
c. 2.824
d. 2.836
3. Sebuah kerucut tingginya 15 cm. Jika volume kerucut tersebut 6.930 cm³, maka diameter kerucut tersebut .... cm
a. 42
b. 43
c. 44
d. 45
4. Sebuah kerucut luas alasnya 154 cm2. Jika volumenya 770 cm³, maka tinggi kerucut tersebut .... cm
a. 12
b. 14
c. 15
d. 16
5. Luas permukaan kerucut dengan diameter 40 cm dan tinggi 15 cm adalah ….
a. 750 π cm²
b. 800 π cm²
c. 850 π cm²
d. 900 π cm²
6. Diketahui sebuah kerucut dengan volume 4.312 cm³. Jika jari-jarinya 14 cm, maka tinggi kerucut tersebut .... cm
a. 18
b. 21
c. 24
d. 26
7.
Volume dan luas permukaan bangun di atas adalah ....
a. V = 1.232 cm³, L = 700 cm²
b. V = 1.232 cm³, L = 702 cm²
c. V = 1.232 cm³, L = 704 cm²
d. V = 1.232 cm³, L = 706 cm²
8. Rumus luas permukaan kerucut adalah ....
a. L = luas alas + luas selimut
b. L = π x r² + π x r x s
c. L = πr x (r + s)
d. a, b, dan c benar
KESIMPULAN
Demikianlah materi kita hari ini semoga bisa di pahami, kalau memang belum paham silahkan bertanya langsung ke ibu.



Tidak ada komentar:
Posting Komentar