Hari/ Tanggal : Jumat, 19 November 2021
Kelas : 8F
Materi : Sistem Persamaan Linier Dua Variabel
KOMPETENSI DASAR
3.2
Tujuan Pembelajaran :
Siswa diharapkan dapat:
- Membedakan persamaan linier satu variabel dan persamaan linier dua variabel
Assalamualaikum anak- anak yang sholeh sholehah....
Apa kabarnya hari ini ?
Semoga kita semua dalam lindungan Allah SWT Aamiin.....
Dan jangan lupa tetap selalu menjaga kesehatan dan selalu memakai prokes nya ya nak.
Baiklah sebelum kita melaksanakan pembelajaran di pagi ini, alangkah baiknya kita awali dengan melaksanakan sholat dhuha dan murojaahnya terlebih dahulu ya nak, dan tak lupa setelah itu pembacaan asmaul husna dan doa belajar ya supaya ilmu yang dipelajari hari ini akan bermanfaat, mudah diterima dan akan berkah ilmunya
Penyelesaian sistem persamaan linear
dua variabel (SPLDV)
Cara penyelesaian SPLDV dapat dilakukan dengan cara :
1. Substitusi
Menggantikan satu variable dengan variable dari
persamaan yang lain.
contoh :
jawab :
Kita ambil persamaan pertama yang akan
disubstitusikan yaitu x + 2y = 8
Kemudian persamaan tersebut kita ubah menjadi x
= 8 – 2y,
Kemudian persamaan yang diubah tersebut
disubstitusikan ke persamaan
2x – y = 6 menjadi :
2 (8 – 2y) – y = 6 à (x persamaan kedua menjadi x = 8 –
2y)
16 – 4y – y = 6
16 – 5y = 6
-5y = 6 – 16
-5y = -10
5y = 10
y = 10/5 = 2
masukkan nilai y=2 ke dalam salah satu persamaan
:
x + 2y = 8
x + 2. 2 = 8
x + 4 = 8
x = 8 - 4
x = 4
2. Eliminasi
Dengan cara menghilangkan salah satu variable x
atau y
contoh :
Selesaikan soal di atas dengan cara eliminasi:
Jawab ;
x + 2y = 8
2x – y = 6
(i) mengeliminasi variable x
5y = 10
y = 10/5
y = 2
masukkan nilai y = 2 ke dalam salah satu
persamaan
x + 2 y = 8
x + 2. 2 = 8
x + 4 = 8
x = 8 – 4
x = 4
(ii) mengeliminasi variable y
x = 20/5
x = 4
masukkan nilai x = 4 ke dalam salah satu
persamaan
x + 2 y = 8
4 + 2y = 8
2y = 8 – 4
2y = 4
y = 4/2
y = 2
3. Grafik
Dengan menggambarkan persamaan linearnya pada
koordinat Cartesius, titik potong dari kedua persamaan linier tersebut
merupakan penyelesaiannya.
Contoh:
Carilah penyelesaian dari:
Jawab:
·
Tentukan titik
potong garis x + y = 8 dengan sumbu x dan sumbu y
·
titik potong dengan
sumbu y jika x = 0
·
jika x = 0 à maka y = 8 – x = 8 – 0 = 8
·
titik potong dengan
sumbu x jika y = 0
·
jika y = 0 à x = 8 – y = 8 – 0 = 8
·
Maka persamaan
garis x + y = 8 adalah melalui titik (0.8) dan (8,0)
·
Tentukan titik
potong garis 2x – y = 4 dengan sumbu x dan sumbu y
·
titik potong dengan
sumbu y jika x = 0
·
jika x = 0 à maka y = 2x – 4 = 2.0 – 4 = - 4
·
titik potong dengan
sumbu x jika y = 0
·
jika y = 0 à2 x = y + 4 = 0 + 4 = 4, maka x = = 2
· Maka persamaan garis 2x – y = 4 adalah melalui titik (0, -4) dan (2,0)
dari gambar grafik terlihat titik potong garis x
+ y = 8 dan 2x – y = 4 adalah (4,4).
Contoh soal penggunaan sistem persamaan linear dua variabel :
Harga 2 buah mangga dan 3 buah jeruk adalah
Rp. 6000, kemudian apabila harga untuk membeli 5 buah mangga dan 4 buah
jeruk adalah Rp11.500,-. Berapa jumlah uang yang harus dibayar apabila
kita akan membeli 4 buah mangga dan 5 buah jeruk ?
Jawab :
Dalam menyelesaikan persoalan cerita seperti di
atas diperlukan penggunaan
model matematika.
Misal: harga 1 buah mangga adalah x dan harga
1 buah jeruk adalah y
Maka model matematika soal tersebut di atas
menjadi :
2x + 3 y = 6000
5x + 4 y = 11500
Ditanya 4 x + 5 y = ?
Kita eliminasi variable x :
masukkan ke dalam salah satu persamaan :
2x + 3 y = 6000
2x + 3 . 1000 = 6000
2x + 3000 = 6000
2x = 6000 – 3000
2x = 3000
x = 1500
didapatkan x = 1500 (harga sebuah mangga) dan y
= 1000 (harga sebuah jeruk) sehingga uang yang harus dibayar untuk membeli 4
buah mangga dan 5 buah jeruk adalah
4 x + 5 y = 4. 1500 + 5. 1000
= 6000 + 5000
= Rp. 11.000,-
Untuk lebih jelas dengan materi ini, silahkan anak anak kerjakan latihan di bawah ini
LATIHAN
1. Rina membeli 3 kg apel dan 2 kg jeruk. Uang yag harus dibayarkan adalah Rp 65.000,00.
Jika diubah menjadi persamaan linear dua variabel, maka pernyataan tersebut menjadi ....
a. 3x + 2y = 65.000
b. 3x – 2y = 65.000
c. 3x + 2y = 65
d. 3x – 2y = 65
2. Himpunan penyelesaian dari sistem persamaan
x + y = 12,
x – y = 4 adalah ....
a. { 4 , 8 }
b. { 12 , 4 }
c. { 4 , 12 }
d. { 8 , 4 }
3. Himpunan penyelesaian dari sistem persamaan
x - y = 6,
x + y = 10 adalah ....
a. {8 , 2}
b. {2 , 8}
c. {6 , 10}
d. {10 , 6}
4. Himpunan penyelesaian dari sistem persamaan
2x - 5y = 1,
4x – 3y = 9 adalah ...
.
a. {1, 3 }
b. {2, 5 }
c. {3, 1 }
d. {4, 3 }
a. {4 , -4}
b. {2 , 0}
c. {2 , 3}
d. {2 , -2}



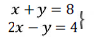

Assalamualaikum
BalasHapusNama Bilal pratama
Kls8f
Ket Hadir
Terimakasih 🙏
Assalamualaikum
BalasHapusNama albhi zafaran
Kls8f
Ket Hadir
Terimakasih 🙏
Assalamualaikum,
BalasHapusNama:Kayla Assyfa Listhon
Kelas:8F
Hari/tanggal:Jum'at/19 November 2021
Terimakasih bu.
Wassalamu'alaikum.
Assalamualaikum
BalasHapusSafira Azzahra
8F
Hadir
Terimakasih
Wassalamu'alaikum
Assalamualaikum
BalasHapusWafa Aziza
8F
Hadir
Assalamualaikum
BalasHapusNama Alvin Aditya Nugraha
Kls8f
Ket Hadir
Terimakasih 🙏
Assalammualaikum
BalasHapusNama:Zullia Ade Rono W
Kelas:8F
Hadir
Terima kasih
Assalamualaikum Wr.Wb.
BalasHapusSaya Khalista Sheila Lathifah.
Dari kelas 8 F.
Hari/Tanggal: Jum’at, 19 November 2021.
Terimakasih bu atas materinya🙏🏻.
Wassalamu'alaikum Wr.Wb.
adzkia mutiara dermawan
BalasHapus8F
hadir
Assalamu'alaikum
BalasHapusNama : Sabina laiqa derina
Kls : 8F
Ket : Hadir
Terimakasih
Assalamualaikum Wr.Wb.
BalasHapusNama saya Khalisa Putri Mukhbita
Dari kelas 8F || Absen : 12
Keterangan: Hadir mengikuti pembelajaran
Hari/Tanggal : Jum'at, 19 November 2021.
Terimakasih bu atas materinya 🙏🏻.
Wassalamualaikum Wr.Wb.
Assalamualaikum
BalasHapusNama were fadhil a
Kls 8F
Hadir
Assalamualaikum
BalasHapusNama : Arga aditya
Kelas : 8F
Ket : hadir
Terimakasih
Wassalamualaikum wr wb
Assalamualaikum wr wb
BalasHapusNama:Raytama Aldino Putra
Kelas:8F
Ket hadir
Wassalmualaikum wr wb
Assalamualaikum
BalasHapusNama : Muhammad Yusuf Isa
Kelas : 8F
Terimakasih
Bagini arya fadila
BalasHapus8f
Hadir