KERUCUT

MATERI HARI SELASA KELAS 9D,9C(10-3-20)

KERUCUT

Pengertian Kerucut

Kerucut merupakan salah satu bangun ruang yang memiliki sebuah alas yang berbentuk lingkaran dengan selimut yang mempunyai irisan dari lingkaran.

Di dalam geometri, kerucut merupakan sebuah limas istimewa yang memiliki alas lingkaran. Kerucut mempunyai 2 sisi dan 1 rusuk. Sisi tegak kerucut tidak berwujud segitiga namun berwujud bidang miring yang disebut sebagai selimut kerucut.

Yang membedakan antara limas dengan kerucut yaitu alas kerucut memiliki bentuk lingkaran, sementara pada limas berbentuk segi n beraturan.

Unsur-unsur Kerucut



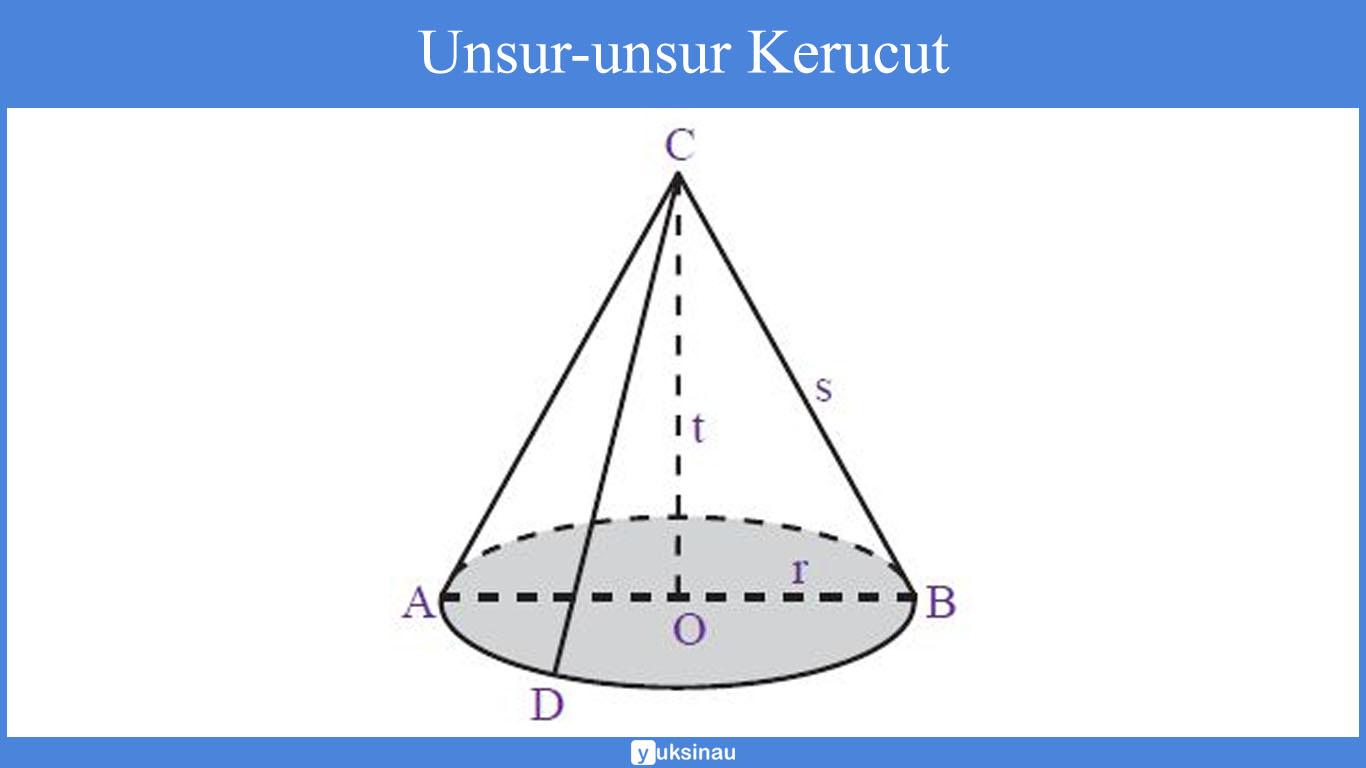
luas permukaan kerucut
1. Bidang alas, yakni sisi yang berbentuk lingkaran (daerah yang diraster).
2. Diameter bidang alas (d), merupakan ruas garis AB.
3. Jari-jari bidang alas (r), merupakan garis OA serta ruas garis OB.
4. Tinggi kerucut (t), yakni jarak dari titik puncak kerucut ke pusat bidang alas (ruas garis CO).
5. Selimut kerucut, merupakan sisi kerucut yang tidak diraster.
6. Garis pelukis (s), merupakan garis-garis pada selimut kerucut yang ditarik dari titik puncak C ke titik pada lingkaran.

Sifat Kerucut

Terdapat beberapa sifat pada bangun ruang kerucut, antara lain ialah sebagai berikut:

1. Kerucut memiliki 2 sisi.
2. Kerucut tidak  memiliki rusuk.
3. Kerucut memiliki 1 titik sudut.
4. Jaring-jaring kerucut terdiri atas lingkaran serta segitiga.
5. Tidak memiliki bidang diagonal
6. Tidak memiliki diagonal bidang

Rumus pada bangun ruang kerucut

1. Rumus untuk menghitung volume:



2. Rumus untuk menghitung luas:
luas alas+luas selimut

Keterangan:

r = jari – jari (cm)
T = tinggi(cm)
π = 22/7 atau 3,14

Jaring-jaring kerucut

Berikut ini merupakan salah satu contoh jaring-jaring pada kerucut





Contoh

1. Sebuah lingkaran memiliki luas 40 cm². Jika lingkaran tersebut dibuat menjadi kerucut dengan tinggi 9 cm, hitung volume kerucut tersebut.

Jawab:

Diketahui:

t = 9 cm

Luas : L = π x r² = 40 cm²

V = 1/3 x π x r² x t

= 1/3 x 40 x 9 (ingat : π x r² = 40 cm²)

= 120 cm³.

Jadi, volume kerucut adalah 120 cm³.

2. Sebuah kerucut memiliki panjang jari-jari alas yaitu 6 cm dan tinggi 8 cm. Berapakah luas kerucut tersebut ( π = 3,14).

Jawab :

r = 6cm

t = 8 cm

s² = r² + t²

s² = 6²+ 8² = 36 + 64 = 100

s =√100 = 10

Luas sisi kerucut = πr(r + s)

= 3,14 x 6 x (6 + 10) = 3,14 x 6 x l6 = 301,44

Maka, luas sisi kerucut yaitu 301,44 cm²