KESEBANGUNAN PADA SEGITIGA

MATERI HARI JUMAT KELAS 9F,9G(31-1-20)

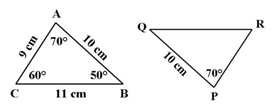
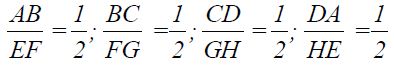Rumus Kesebangunan pada Segitiga

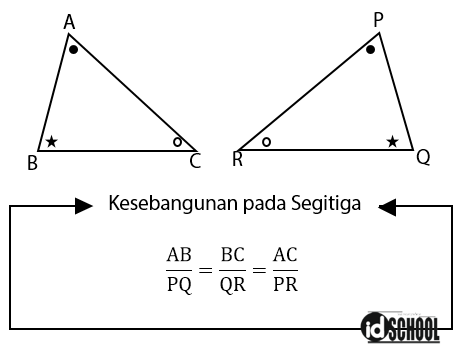
Kesebangunan pada Segitiga:

Bentuk 1: kesebangunan pada segitiga

  

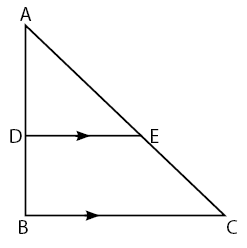
atau

  

 Bentuk 2: kesebangunan pada segitiga

  

  

  

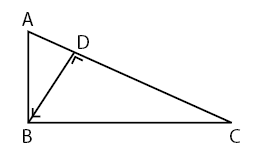
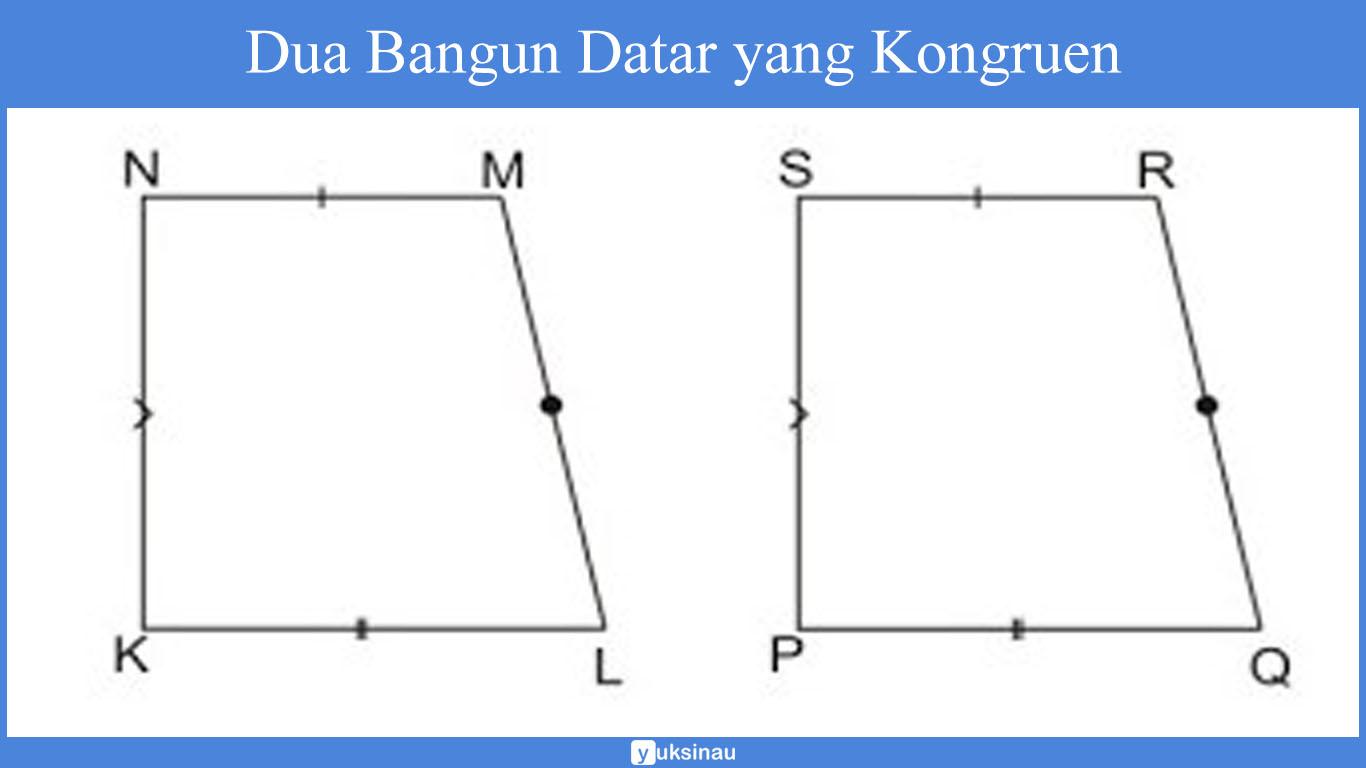
Berikutnya adalah kesebangunan pada bidang datar segi empat yaitu bangun datar berbentuk trapesium. Ada dua bentuk yang perlu sobat idschool ketahui.

 Kesebangunan pada Trapesium

Bentuk 1: kesebangunan pada trapesium

  

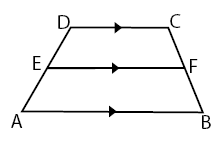
atau

  

 Bentuk 2: kesebangunan pada trapesium

  

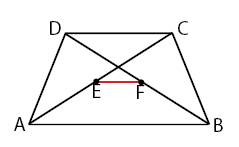
Keterangan: E dan F berturut-turut adalah titik tengah AC dan BD.

Kedua rumus kesebangunan pada trapesium di atas diperoleh melalui penyederhanaan persamaan. 

Contoh 1

Febri mempunyai tinggi badan 150 cm. Ia berdiri pada titik yang berjarak 10 m dari sebuah gedung. Ujung bayangan Febri berimpit dengan ujung bayangan gedung. Jika panjang bayangan Febri adalah 4 m, maka tinggi gedung adalah ….
A. 5,25 m
B. 5,50 m
C. 6,25 m
D. 6,75 m
SOAL UN MATEMATIKA SMP 2016

Pembahasan:

Perhatikan gambar berikut!

Perhatikan segitiga ABE dan segitiga ACD!

Berdasarkan prinsip kesebangunan dapat diperoleh

  

Sehingga,

  

  

  

Jawaban: A

Contoh 2

Perhatikan gambar berikut!

Jika CF : FB = 2 : 3 dan CD = 12 cm, maka panjang EF adalah …. (SOAL UN MATEMATIKA SMP 2016)

A.       6 cm
B.       9 cm
C.       12 cm
D.       18 cm

Pembahasan:

Berdasarkan keterangan pada soal, kita dapat mengetahui ukuran masing-masing sisi, seperti terlihat pada gambar berikut.

 Untuk menghitung EF, gunakan rumus di bawah.

  

Sehingga,

  

  

  

Jawaban: D

SOAL POST TEST

HARI JUMAT KELAS 9F,9G(24-1-20)

KERJAKAN SOAL-SOAL DI BAWAH INI!!!

1. Perhatikan gambar berikut!

Pada bangun persegi panjang ABCD dan PQRS di atas adalah sebagun. Tentukan:

a. Panjang PQ
b. Luas dan keliling persegi panjang PQRS

2. Perhatikan gambar berikut!

Tentukan Panjang DB

3. Perhatikan gambar segitiga dibawah ini!

Tentukan QR dan QU

4. Perhatikan gambar berikut.

Tentukan panjang DE!

5.  Perhatikan segitiga dibawah ini!

Jika telah diketahui panjang SR adalah 8 cm, tentukan panjang QS!

DUA SEGITIGA YANG KONGRUEN

MATERI HARI SENIN KELAS 9H,9D(20-1-20)

Dua Segitiga Yang Kongruen

Secara geometris dua segitiga yang kongruen ialah dua segitiga yang saling menutupi dengan tepat. Sifat dua segitiga kongruen tersebut, yaitu:

a. Pasangan sisi yang bersesuaian adalah sama panjang
b. Sudut yang bersesuaian adalahsama besar

Segitiga dapat dikatakan kongruen mana kala dapat memenuhi syarat yskni sebagai berikut:

a. Tiga Sisi yang Bersesuaian Sama Besar (sisi, sisi, sisi)

Berdasarkan gambar dari segitiga ABC serta segitiga PQR di atas, diketahui jika keduanya mempunyai panjang AB = PQ, panjang AC = PR, serta panjang BC = QR. 

b. Sudut dan Dua Sisi yang Bersesuaian Sama Besar (sisi, sudut, sisi)

Berdasarkan dari gambar bangun segitiga ABC serta segitiga PQR di atas, diketahui jika kedua bangunnya memiliki sisi AB = PQ, ∠B = ∠Q, dan juga sisi BC = QR

c. Satu Sisi Apit dan Dua Sudut yang Bersesuaian Sama Besar (sudut, sisi, sudut)

Berdasarkan dari gambar bangun segitiga ABC dan segitiga PQR di atas, diketahui bahwa, ∠A = ∠P, sisi AC = PR, serta ∠Q = ∠R.

Contoh 1

Perhatikan gambar berikut.

Jika ΔABC kongruen dengan ΔPQR, maka tentukan:
- panjang PR
- panjang QR
- ∠PQR
- ∠QRP

Penyelesaian:

• Oleh karena sisi PR bersesuaian dengan AC, maka panjang sisi PR = AC = 9 cm.
• Oleh karena sisi QR bersesuaian dengan CB, maka panjang QR = CB = 11 cm.
• Oleh karena ∠PQR bersesuaian dengan ∠ABC, maka ∠PQR = ∠ABC = 50⁰.
• Oleh karena ∠QRP bersesuaian dengan ∠ACB, maka ∠ QRP = ∠ ACB = 60⁰.

Perbedaan antara Kesebangunan dan Kekongruenan pada Segitiga

KESEBANGUNAN DAN KEKONGRUENAN

MATERI HARI JUMAT KELAS 9F,9G ( 10-1-20)

Pengertian Kesebangunan Bangun Datar

Kesebangunan merupakan sebuah bangun datar di mana sudut – sudutnya mempuntai kesesuaian yang sama besarnya. Dan juga panjang sisi – sisi sudutnya juga bersesuai dengan mempunyai sebuah perbandingan yang sama.

Perhatikan contoh di bawah ini:

Dua Bangun Datar yang Sebangun

Sekarang, coba kamu perhatikan Gambar di atas! Sebangunkah persegipanjan ABCD dengan persegipanjang EFGH? Pada persegipanjang ABCD dan persegipanjang EFGH, perbandingan panjangnya adalah 4 : 8 = 1 : 2.

Adapun perbandingan lebarnya adalah 2 : 4 = 1 : 2. Dengan demikian, perbandingan sisi-sisi yang bersesuaian pada kedua persegipanjang tersebut dapat dinyatakan sebagai berikut.

Kemudian, perhatikan sudut-sudut yang bersesuaian pada persegipanjang ABCD dan persegipanjang EFGH. Oleh karena keduanya berbentuk persegipanjang, setiap sudut besarnya 90° sehingga sudut-sudut yang bersesuaian pada kedua bangun tersebut sama besar.

Pengertian Kekongruenan

Kekongruenan merupakan dua buah bangun datar yang di mana kedua bangunnya sama – sama memiliki bentuk dan juga ukuran yang sama.

Kekongruenan ini biasa dilambangkan dengan pemakaian simbol ≅.

Perhatikan contoh di bawah ini:

1. Dua Bangun Datar yang Kongruen

Pada kedua bangun di atas adalah bangun yang kongruen, karena panjang KL = PQ, Panjang LM = QR, panjang MN = RS, panjang NK = SP maka oleh karena itu, pada bangun KLMN dan PQRS dapat dikatakan adalah kongruen karena memiliki bentuk dan ukuran yang sama.

Perbedaan Kesebangunan dan Kekongruenan

Hal mendasar yang membedakan kongruen dan sebangun yaitu:

Bangun dikatakan kongruen jika sisi-sisi yang bersesuaian harus sama panjang. Sementaa jika bangun dikatakan sebangun apabila perbandingan sisi-sisi yang bersesuaian harus sama besar.

Sehingga dapat kita simpulkan bahwa, seluruh bangun yang kongruen sudah pasti sebangun, namun jika sebangun belum tentu kongruen.